William Wallace Proof of the Butterfly Theorem
In a letter to William Wallace, dated 7 April 1805, Sir William Herschel - the discoverer of Uranus and its two major moons, Titania and Oberon - wrote:
I have kept a little problem for you which a friend of mine has sent me who says he cannot find a solution of it. I mentioned to him that I had a friend who would probably help him to one. The problem is this. Given AB the diameter of a circle. CD a chord cutting it at right angles in K. EF, and HG two other chords drawn any how through the point K; and HF, EG chords joining the extremes of EF, HG. Required to prove that MK is equal to LK.

Until very recently, this is the first recorded mention of the Butterfly theorem. The previous record, according to [Coxeter and Greitzer] was the 1815 solution by W. G. Horner of Horner's method fame. Wallace solution appears to predate that of Horner by 10 years. Sir Herschel's letter may has been thought to be the original source of the problem. However, the latest discovery of a 1803 publication with W. Wallace's posting of a generalization of the problem shows convincingly that Wallace has been aware of the problem that is known now as the "Butterfly Theorem" as early as 1802.
What follows is the original solution by William Wallace as was recently published in the Journal of the British Society for the History of Mathematics:
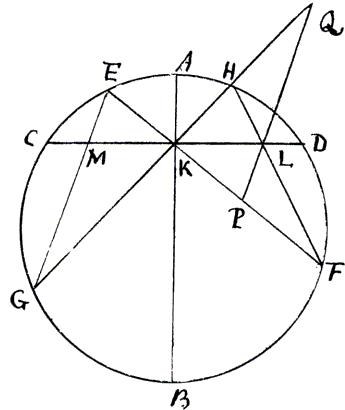
Through L draw PQ parallel to GE, meeting KF in P and KH in Q.
Because of the parallels the angle HQP is equal to HGE, but HGE is equal to HFE, or to HFP, for they are in the same segment, therefore the angles HQP, HFP are equal, and hence the points H, Q, F, P are in the circumference of a circle, wherefore
The triangles KEG, KPQ are similar and their sides EG, PQ are similarly divided by the lines KM, KL, which lines are to each other as EM to PL, and as MG to LQ, therefore
| KM² : EM × MG :: KL² : PL × LQ, or FL × LH; | ||
| and by composition, &c. | KM² : KM² + CM × MD :: KL² : KL² + CL × LD. |
But KM² + CM × MD = CK² and KL² + CL × LD = KD².
Therefore KM² : CK² :: KL² : KD², and KM : CK :: KL : KD.
But CD being perpendicular to the diameter, KC is equal to KD, therefore KM must also be equal to KL as was to be demonstrated.
Remark
The above proposition is a particular case of a more general one extending to all the Conic Sections, which may be expressed thus. If AB is any diameter of a Conic Section, and CD any right line cutting it in K, and parallel to a tangent at its vertices; also EF and HG two other lines drawn anyhow through K, to meet the conic section, the one in the points E, F, and the other in the points G, H, the straight lines EG, FH which join the extremities of these lines shall intercept upon CD the segments KM, KL which are equal to each other.
W Wallace
Reference
- H. S. M. Coxeter, S. L. Greitzer, Geometry Revisited, MAA, 1967
- Alex D D Craik and John J O'Connor, Some unknown documents associated with William Wallace (1768-1843), BSHM Bulletin: Journal of the British Society for the History of Mathematics, 26:1, 17-28
Butterfly Theorem and Variants
- Butterfly theorem
- 2N-Wing Butterfly Theorem
- Better Butterfly Theorem
- Butterflies in Ellipse
- Butterflies in Hyperbola
- Butterflies in Quadrilaterals and Elsewhere
- Pinning Butterfly on Radical Axes
- Shearing Butterflies in Quadrilaterals
- The Plain Butterfly Theorem
- Two Butterflies Theorem
- Two Butterflies Theorem II
- Two Butterflies Theorem III
- Algebraic proof of the theorem of butterflies in quadrilaterals
- William Wallace's Proof of the Butterfly Theorem
- Butterfly theorem, a Projective Proof
- Areal Butterflies
- Butterflies in Similar Co-axial Conics
- Butterfly Trigonometry
- Butterfly in Kite
- Butterfly with Menelaus
- William Wallace's 1803 Statement of the Butterfly Theorem
- Butterfly in Inscriptible Quadrilateral
- Camouflaged Butterfly
- General Butterfly in Pictures
- Butterfly via Ceva
- Butterfly via the Scale Factor of the Wings
- Butterfly by Midline
- Stathis Koutras' Butterfly
- The Lepidoptera of the Circles
- The Lepidoptera of the Quadrilateral
- The Lepidoptera of the Quadrilateral II
- The Lepidoptera of the Triangle
- Two Butterflies Theorem as a Porism of Cyclic Quadrilaterals
- Two Butterfly Theorems by Sidney Kung
- Butterfly in Complex Numbers
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73601453
