Another synthetic proof of
the butterfly theorem using
the midline in triangle

Tran Quang Hung
Forum Geometricorum, Volume 16 (2016) 345–346

Let $M\;$ be the midpoint of a chord $AB\;$ of a circle. Through $M\;$ two other chords $CD\;$ and $EF\;$ are drawn. If $C\;$ and $F\;$ are on opposite sides of $AB,\;$ and $CF,\;$ $DE\;$ intersect $AB\;$ at $G\;$ and $H\;$ respectively, then $M\;$ is also the midpoint of $GH.$

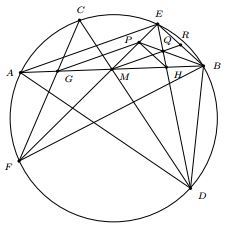
Let $P\;$ be the point on segment $ME\;$ such that $GP\parallel AE.\;$ $PB\;$ intersects $EH\;$ at $Q.\;$ We have

$\angle PGB = \angle EAB = \angle EFB = \angle PFB.$

This shows that quadrilateral $FGPB\;$ is cyclic. We get

$\angle QBM = \angle PBG = \angle PFG = \angle EFC = \angle EDC = \angle QDM.$

Therefore, quadrilateral $DMQB\;$ is also cyclic. From this,

$\angle QMB = \angle QDB = \angle EDB = \angle EAB,$

and $MQ\parallel AE.\;$ Since $M\;$ is the midpoint of $AB,\;$ by the midline theorem, $MQ\;$ passes through the midpoint $R\;$ of $EB.\;$ By Ceva's theorem for $\Delta MEB\;$ and Thales's theorem for $\Delta MEA,\;$ we get $\displaystyle\frac{MH}{MB} = \frac{MP}{ME} = \frac{MG}{MA}.\;$ Since $MA = MB,\;$ we also have $MG = MH.$

Butterfly Theorem and Variants

1. Butterfly theorem
2. 2N-Wing Butterfly Theorem
3. Better Butterfly Theorem
4. Butterflies in Ellipse
5. Butterflies in Hyperbola
6. Butterflies in Quadrilaterals and Elsewhere
7. Pinning Butterfly on Radical Axes
8. Shearing Butterflies in Quadrilaterals
9. The Plain Butterfly Theorem
10. Two Butterflies Theorem
11. Two Butterflies Theorem II
12. Two Butterflies Theorem III
13. Algebraic proof of the theorem of butterflies in quadrilaterals
14. William Wallace's Proof of the Butterfly Theorem
15. Butterfly theorem, a Projective Proof
16. Areal Butterflies
17. Butterflies in Similar Co-axial Conics
18. Butterfly Trigonometry
19. Butterfly in Kite
20. Butterfly with Menelaus
21. William Wallace's 1803 Statement of the Butterfly Theorem
22. Butterfly in Inscriptible Quadrilateral
23. Camouflaged Butterfly
24. General Butterfly in Pictures
25. Butterfly via Ceva
26. Butterfly via the Scale Factor of the Wings
27. Butterfly by Midline
28. Stathis Koutras' Butterfly
29. The Lepidoptera of the Circles
30. The Lepidoptera of the Quadrilateral
31. The Lepidoptera of the Quadrilateral II
32. The Lepidoptera of the Triangle
33. Two Butterflies Theorem as a Porism of Cyclic Quadrilaterals
34. Two Butterfly Theorems by Sidney Kung
35. Butterfly in Complex Numbers

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny