Six Concyclic Points on Sides of a Triangle

In $\Delta ABC$ points $A_1,A_2$ lie on $BC,$ $B_1,B_2$ lie on $AC,$ $C_1,C_2$ lie on $AB,$ such that $A_1,A_2,B_1,B_2$ are concyclic as are $A_1,A_2,C_1,C_2$ and $B_1,B_2,C_1,C_2.$

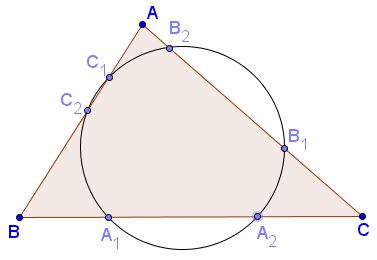
Six Concyclic Points on Sides of a Triangle - problem

Prove that all six points lie on a circle.

Proof

[Pedoe, p. 113]. Circles $(A_{1}A_{2}B_{1}B_{2})$ and $(A_{1}A_{2}C_{1}C_{2})$ have $A_{1}A_{2},$ i.e., $BC$ as the radical axis. Similarly, $AC$ serves as the radical axis of $(A_{1}A_{2}B_{1}B_{2})$ and $(B_{1}B_{2}C_{1}C_{2}),$ while $AB$ is the radical axis of $(A_{1}A_{2}C_{1}C_{2})$ and $(B_{1}B_{2}C_{1}C_{2}).$ But the pairwise radical axes of any three circles are known to concur at their radical center. Having them form a triangle leads therefore to a contradiction.

Like another Six Concyclic Points theorem, this one too can be used to proving the existence of the 9-Point Circle.

It is known that the circles on the sides of a triangle as diameters pass through the feet of the altitudes to the remaining sides:

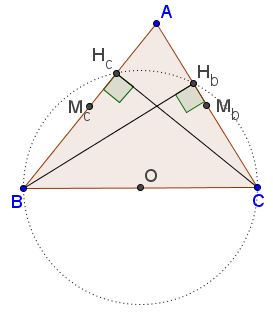
Six Concyclic Points on Sides of a Triangle - application

By the Power of a Point theorem, $AH_{c}\cdot AB=AH_{b}AC,$ where $H_{b},H_{c}$ are the feet of two altitudes in $\Delta ABC.$ If $M_{b},M_{c}$ are the corresponding midpoints of the sides then

$\displaystyle AH_{c}\cdot AM_{c}=AH_{c}\frac{AB}{2}=AH_{b}\frac{AC}{2}=AH_{b}\cdot AM_{b},$

implying that $H_{b},M_{b},H_{c},M_{c}$ are concyclic. Applying the same consideration to the other pairs of the sides of $\Delta ABC$ puts us into the framework of the theorem just proved, with the conclusion that the midpoints and the feet of the altitudes in a triangle are concyclic.

Acknowledgment

I was reminded of this theorem by Telv Cohl at CutTheKnotMath facebook page who referred to it as David's. I could not verify this designation independently.

References

D. Pedoe, Geometry: A Comprehensive Course, Dover, 1988

Radical Axis and Radical Center

71868292