Algebraic proof of the theorem of butterflies in quadrilaterals

Fan Tai-Sheng
February 5, 2011
Republic of China (Taiwan)

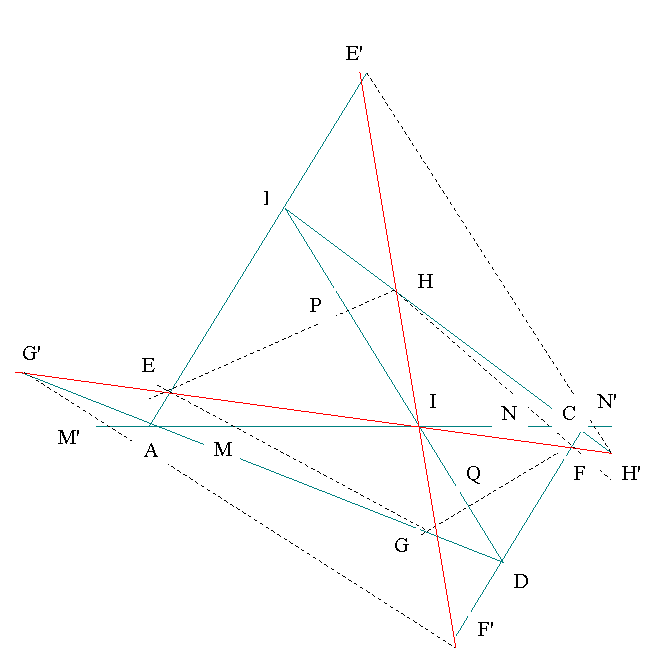
In the figure, in Cartesian coordinates, let AC lie on the x-axis, with I being the origin, and points A,B,C,D be (-a, 0), (-e, b), (c, 0), (ed, -bd) respectively. Then the sides AB, CD, BC and AD are represented by equations

AB: b(x + a) + (e - a)y = 0
CD: bd(x - c) + (de - c)y = 0
BC: b(x - c) + (c + e)y = 0
AD: bd(x + a) + (de + a)y = 0.

Since the lines EF and GH both pass through the origin I, they can be given by equations

EF: y - m₁x = 0 and
GH: y - m₂x = 0,

where m₁ and m₂ are the slopes of EF and GH respectively. Extend EF to cut the sides BC and AD at H' and G' respectively and also extend GH to cut the sides AB and CD at E' and F' respectively.

Now it can be easily seen that for parameters λ and μ, the equation

describes the pencil of quartic curves that pass through the eight points E, F, G, H, E', F', G' and H'. Further, there exist some constant λ and μ such that a degenerate quartic curve of four straight lines passing through these points is uniquely determined. Hence we can choose the constants λ and μ such that the degenerate quartic function f(x, y) describes the four straight lines EG, FH, F'G' and E'H':

Now it can be seen in the figure that the line y = 0 cuts the four lines EG, FH, F'G' and E'H' at the points M, N, M' and N' respectively.

Hence the equation

f(x, 0) = λb⁴d²(x + a)²(x - c)² + μm₁²m₁²x⁴ = 0

has four real roots {IM, IN, -IM', IN'} if λ and μ are oppositely signed. Setting μm₁²m₁² /λb⁴d² = -k²; the equation is equivalent to

(x + a)²(x - c)² - k²x⁴ = 0.

Factoring the left-hand side gives two quadratic equations:

(1 + k)x² + (a - c)x - ac = 0 and
(1 - k)x² + (a - c)x - ac = 0.

Now it is obvious that the roots, say, x and x' of either of the two quadratic equations satisfy the following relation

1/x + 1/x' = (x + x')/xx' = -(a - c)/(1 ± k)/(-ac)/(1 ± k) = 1/c - 1/a.

Therefore it can be concluded that 1/IN - 1/IM = 1/IN' - 1/IM' = 1/IC - 1/IA is constant, namely,

Now, by symmetry, it can be easily seen that in the figure, the intersections P and Q of lines EH and FG with the diagonal BD respectively have a similar property such that

The quadrilateral ABCD itself can be seen as composed of two butterflies ACDBA and BDACB which both with their wing tips touching both diagonals AC and BD satisfy both equations (1) and (2). If we connect intersections inside the quadrilateral and extend lines to create intersections outside it we can get infinitely many butterflies which all have the properties of being invariant under the equations (1) and (2).

From the proof above it can be seen that the quadrilateral doesn’t have to be convex. Actually, butterflies inhabit in any quadrilateral defined by four points in general position, only the distances in equations (1) and (2) are signed according to the orientation of the line.

Butterfly Theorem and Variants

1. Butterfly theorem
2. 2N-Wing Butterfly Theorem
3. Better Butterfly Theorem
4. The Lepidoptera of the Circles
5. The Lepidoptera of the Quadrilateral
6. The Lepidoptera of the Quadrilateral II
7. Butterflies in Ellipse
8. Butterflies in Hyperbola
9. Butterflies in Quadrilaterals and Elsewhere
10. Pinning Butterfly on Radical Axes
11. Shearing Butterflies in Quadrilaterals
12. The Plain Butterfly Theorem
13. Two Butterflies Theorem
14. Two Butterflies Theorem II
15. Two Butterflies Theorem III
16. Algebraic proof of the theorem of butterflies in quadrilaterals
17. William Wallace's Proof of the Butterfly Theorem
18. Butterfly theorem, a Projective Proof
19. Areal Butterflies
20. Butterflies in Similar Co-axial Conics

|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|

Copyright © 1996-2012 Alexander Bogomolny