Copernicus' Theorem

Consider two circles of radii R and R/2 with the smaller one rolling inside the bigger circle without slipping. Copernicus' Theorem states a surprising result that a point on the circumference of the small circle traces a straight line segment - a diameter of the big circle, to be precise.

The proof also describes in mathematical terms the meaning of the motion without slipping. Let the point P be the current point of contact of the two circles. Assume point M on the small circle has previously occupied the position of point N on the large circle. Since there is no slipping, arcs PM (on the small circle) and PN (on the large circle) have exactly the same length. The central PON equals the angular measure of the arc PN. The inscribed POM equals half the angular measure of the arc PM. The two arcs have the same length but belong to circles whose radii differ by a factor of 2. Therefore, the angular measure of the arc PN is half that of the arc PM. It then follows that PON = POM. Therefore, the point M lies on the straight line ON.

A related problem deals with a sliding segment of fixed length whose endpoints remain on the two axes of a Cartesian coordinates system. Imagine a circle drawn on the moving segment as on the diameter, and another, fixed one, of double radius centered at the origin. From Copernicus' Theorem, two points that span a diameter of the moving circle trace two perpendicular diameters of the stationary circle. (The diagram on the right is clickable - try it.)

The center of the moving segment (now looked at as the center of the small circle) obviously traces a circle around the origin. Other points on the segment trace ellipses of various shapes. What about other points that may be attached to the moving segment?

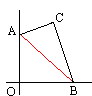
For example, let AB denote the segment. Construct a right-angled triangle ABC. What is the locus of points C with A and B, as before, sliding along the two axes?

Constructing the two circles, we note that, since ACB is right, the point C lies on the circumference of the moving circle. Therefore, according to Copernicus' Theorem, it traces a straight line - one of the diameters of the stationary circle.

We may generalize the problem. Fix three points A,B, and C on the circumference of the moving circle. By Copernicus' Theorem, each of the points traces a straight line. The lines are not necessarily perpendicular. Let's go backwards. Start with two not necessarily perpendicular lines OA and OB. Imagine a segment AB of fixed length move with its endpoints on the two lines. Construct ABC. To make Copernicus' Theorem applicable, we need C to lie on the circumference of a circle that passes through A and B but also through the point O. Quadrilaterals with vertices on a circle are known as cyclic. For cyclic quadrilaterals, we have

AOB + ACB = 180o.

Now, choose any C that satisfies ACB = 180^o - AOB. So chosen point C will trace a straight line segment. We have solved the following problem:

Given two straight lines OA and OB. Consider ABC such that ACB = 180o - AOB. Find the locus of points C when A and B slide along the given straight lines.

Finally, Copernicus' theorem is a particular case of the Double Generation Theorem discovered by Daniel Bernoulli in 1725.