Butterfly Trigonometry

Butterflies in quadrilaterals are not much different from butterflies living in circles. And the proof of their existence is readily reduced by affine transformation (shearing) to the case of orthodiagonal quadrilaterals. Two additional (trigonometric) proofs supplied by Sidney Kung (August 13, 2012) establish beyond any doubts the presence of butterflies in orthodiagonal (hence, in other, too) quadrilateral.

Theorem

Through the intersection \(O\) of the mutually perpendicular diagonals \(RS\), \(PQ\) of a convex quadrilateral \(RQSP\), draw two lines \(AB\) and \(CD\) that meet the sides of \(RQSP\) at \(A\), \(B\), \(C\), \(D\). If \(X = AD \cap PQ\), \(Y=CB\cap PQ\), and if \(OP = OQ\), then \(OX = OY\).

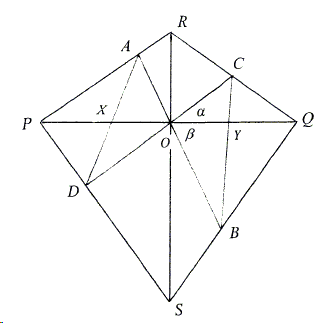
The first proof depends on a lemma proved elsewhere

Lemma 1

Let in \(\triangle RST\), \(RU\) be a cevian through vertex \(R\). Introduce angles \(\alpha = \angle SRU\) and \(\beta = \angle URT\). Then

\( \frac{\mbox{sin}(\alpha + \beta)}{RU} = \frac{\mbox{sin}(\alpha)}{RT} + \frac{\mbox{sin}(\beta)}{RS}. \)

Proof 1 of Theorem

Apply the lemma to triangles \(ROQ\), \(SOQ\), and \(BOC):

(1)	\(\frac{1}{OC}=\frac{\mbox{sin}(\alpha)}{OR}+\frac{\mbox{cos}(\alpha)}{OQ},\)
(2)	\(\frac{1}{OB}=\frac{\mbox{sin}(\beta)}{OS}+\frac{\mbox{cos}(\beta)}{OQ},\)
(3)	\(\frac{\mbox{sin}(\alpha +\beta)}{OY}=\frac{\mbox{sin}(\beta)}{OC}+\frac{\mbox{sin}(\alpha)}{OB}.\)

Combining (1)-(3) we obtain

(4)	\( \frac{\mbox{sin}(\alpha + \beta)}{OY}= \mbox{sin}(\beta)\left(\frac{OQ\cdot \mbox{sin}(\alpha)+OR\cdot \mbox{cos}(\alpha)}{OR\cdot OQ} \right)+ \mbox{sin}(\alpha)\left(\frac{OQ\cdot\mbox{sin}(\beta)+OS\cdot\mbox{cos}(\beta)}{OS\cdot OQ} \right). \)

Similarly, applying Lemma to triangles \(SOP\), \(ROP\), and \(AOD\), we have

(5)	\(\frac{1}{OD}=\frac{\mbox{sin}(\alpha)}{OS}+\frac{\mbox{cos}(\alpha)}{OP},\)
(6)	\(\frac{1}{OA}=\frac{\mbox{sin}(\beta)}{OR}+\frac{\mbox{cos}(\beta)}{OP},\)
(7)	\(\frac{\mbox{sin}(\alpha +\beta)}{OX}=\frac{\mbox{sin}(\beta)}{OD}+\frac{\mbox{sin}(\alpha)}{OA}.\)

Combining (5)-(7) we obtain

(8)	\( \frac{\mbox{sin}(\alpha + \beta)}{OX}= \mbox{sin}(\beta)\left(\frac{OP\cdot \mbox{sin}(\alpha)+OS\cdot \mbox{cos}(\alpha)}{OS\cdot OP} \right)+ \mbox{sin}(\alpha)\left(\frac{OP\cdot\mbox{sin}(\beta)+OR\cdot\mbox{cos}(\beta)}{OP\cdot OR} \right). \)

Remembering that \(OP=OQ\), a comparison of (4) and (8) shows that the right-hand sides are equal, and so are the left-hand sides, implying \(OX=OY\).

Proof 2

Let \(E\) and \(F\) be points symmetric to \(C\) and \(B\) with respect to the line \(RS\). Enlarging the left portion of the diagram

let \(AF\cap OP=Z\). \(F\) being a reflection of \(B\), line \(OP\) bisects \(\angle AOF\). Thus

(9)	\( \frac{AF}{ZF}=\frac{AO}{OF}. \)

Note that triangles \(OFD\) and \(OPD\) are co-side (implying they have the same altitude from \(O\)); it follows that

(10)	\( \frac{DF}{DP}=\frac{1/2\times OD\times OF\times\mbox{sin}(\theta)}{1/2\times OD\times OP\times\mbox{sin}(\alpha)}=\frac{OF\times \mbox{sin}(\theta)}{OP\times\mbox{sin}(\alpha)}. \)

Similarly, since triangles \(OEP\) and \(OEA\) share side \(OE\),

(11)	\( \frac{PE}{EA}=\frac{OP\times \mbox{sin}(\alpha)}{OA\times\mbox{sin}(\theta)}. \)

Multiplying (9), (10), and (11) gives

\( \frac{AZ}{ZF}\frac{DF}{DP}\frac{PE}{EA}=\frac{AO}{OF}\frac{OF}{OP}\frac{OP}{OA}=1. \)

Thus, by the converse of Ceva's Theorem, \(AD\), \(OP\), and \(EF\) are concurrent. Since \(X\) and \(Y\) are on \(PQ\), and \(X\in EF\), \(Y\) must be the symmetric image of \(X\). So, \(OX=OY\).

References

Sidney Kung, A butterfly theorem for quadrilaterals, Math. Mag. 78 (2005), 314

Butterfly Theorem and Variants

49552075