Two Butterflies Theorem as a Porism of Cyclic Quadrilaterals

The following is a part of Jerzy Kocik's paper A porism concerning cyclic quadrilaterals (Geometry, Volume 2013 (Jun 2013), Article ID 483727.)

The main tool of the article, referred there as the reversion in a circle through a point and the associated Möbius transform have been discovered independently by Nathan Bowler in 2002 in his proof of the Two Butterflies Theorem. Jerzy Kocik extends Nathan's result in several ways: explicit matrix representation of the Möbius transform; its application to any straight line, not necessarily a chord in a circle and to any nondegenerate conic section.

Given a circle $\omega\;$ and point $P\notin\omega,\;$ the reversion in the circle $\pi:\;\omega\rightarrow\omega\;$ through $P\;$ is the mapping of $\omega\ni A\mapsto\pi (A)\in\omega,\;$ such that points $A,\;$ $P,\;$ and $\pi (A)\;$ are collinear:

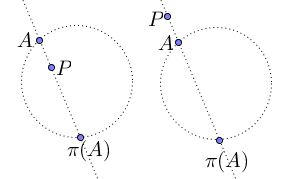
If $P\in\omega\;$ then for any $A\in\omega,\;$ $\pi (A)=P.$

Clearly, for $P\notin\omega,\;$ $\pi\;$ is an involution, $\pi^2=id,\;$ and is, therefore, invertible.

Interpret each point $P\;$ as a complex number $p\in\mathbb{C}.\;$ Without loss of generality, we shall assume that $\omega\;$ is the unit circle, $\omega = \{z\in\mathbb{C}:\; |z|^2 = 1\}.\;$ Complex conjugation is denoted in two ways (an overbar or an asterisks).

Note that the Möbius transform is defined up to a scalar factor and, therefore, so is the associated matrix.

We first check that reversions leave the unit circle invariant: if $|z|=1\;$ then also $|z'|=1:$

$\displaystyle\begin{align} |z'|^2 &= \left(\frac{z-p}{\overline{p}z-1}\right)\left(\frac{z-p}{\overline{p}z-1}\right)^{*}\\ &=\frac{|z|^2-z\overline{p}-p\overline{z}+|p|^2}{|p|^2|z|^2-\overline{p}z-p\overline{z}+1}\\ &=\frac{1-z\overline{p}-p\overline{z}+|p|^2}{|p|^2-\overline{p}z-p\overline{z}+1}\\ &=1. \end{align}$

Next we show that, for any $z\in\omega,\;$ if $z'\ne z,\;$ points $z,p,z'\;$ are collinear.

$\displaystyle\begin{align} \frac{z'-p}{z-p} &= \frac{\displaystyle\frac{z-p}{\overline{p}z-1}-p}{z-p}=\frac{(z-p)-p(\overline{p}z-1)}{(z-p)(\overline{p}z-1)}\\ &=\frac{\overline{z}}{\overline{z}}\frac{z-|p|^2z}{(z-p)(\overline{p}z-1)}\\ &=\frac{1-|p|^2}{\overline{p}z+p\overline{z}-|p|^2-1}\\ &=\frac{1-|p|^2}{2\Re (\overline{p}z)-|p|^2-1}\in\mathbb{R}, \end{align}$

In case $z'=z,\;$ $\displaystyle\frac{z'-p}{z-p}=1,\;$ and from the last line above, $\displaystyle 1=\frac{1-|p|^2}{2\Re (\overline{p}z)-|p|^2-1}\in\mathbb{R}\;$ from which $\Re (\overline{p}z)=1.\;$ So that $\overline{p}z+p\overline{z}=2\;$ and, since $|z|^2=1,\;$ $\overline{(p-z)}z+(p-z)\overline{z}=0,\;$ making $p-z\;$ and $z\;$ perpendicular. This means that $p\;$ lies on the tangent to $\omega\;$ at $z,\;$ implying that $z\;$ is a double point of the reversion.

Here's the statement of the Butterfly Porism:

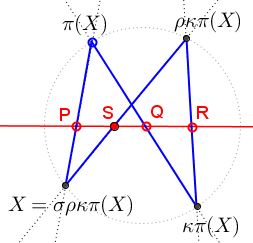
Here's an equivalent version:

Let $\omega\;$ be a circle and $\ell\;$ a line with three points $P,\;$ $Q,\;$ $R.\;$ Let $X\;$ be a point on the circle. The point $S,\;$ the intersection of line $\ell\;$ with line $[\rho\kappa\pi (X), X],\;$ does not depend on $X\in\omega.$

And here is a more general statement:

The composition of three point reversions $\rho\kappa\pi\;$ of a circle is a reversion if and only if points $P,\;$ $Q\;$ and $R\;$ are collinear.

This is the statement we shall proof below.

Consider the product of the consecutive reversions through $P,\;$ $Q,\;$ $R,\;$ as represented by matrices:

$\begin{align}M&=\begin{bmatrix}1&-r\\ \overline{r}&-1\end{bmatrix}\begin{bmatrix}1&-q\\ \overline{q}&-1\end{bmatrix}\begin{bmatrix}1&-p\\ \overline{p}&-1\end{bmatrix}\\ &=\begin{bmatrix}1-\overline{p}q+\overline{q}r-r\overline{p}&-p+q-r+p\overline{q}r\\ \overline{p}-\overline{q}+\overline{r}-\overline{p}q\overline{r}&-1+p\overline{q}-q\overline{r}+\overline{r}p\end{bmatrix}\end{align}$

Note right away that $M_{12}=-\overline{M_{21}}.\;$

Now, since $p,\;$ $q,\;$ $r\;$ are collinear, $r=mp+nq,\;$ where $m+n=1\;$ and $m,n\in\mathbb{R}.\;$ Then $M_{11}=1-m(\overline{p}q+p\overline{q})+m|p|^2-n|q|^2\in\mathbb{R}\;$ and similarly for $M_{22}=-1+m(\overline{p}q+p\overline{q})-m|p|^2+n|q|^2\in\mathbb{R}\;$ such that $M_{11}=-M_{22}.$

Thus $M\;$ corresponds to a Möbius transform and, hence, to a reversion. Since the transform and the matrix are defined up to a scalar, we divide every entry by $M_{11}\;$ to obtain

$\displaystyle M=\begin{bmatrix}1&\frac{-p+q-r+p\overline{q}r}{1-\overline{p}q+\overline{q}r-r\overline{p}}\\ \frac{\overline{p}-\overline{q}+\overline{r}-\overline{p}q\overline{r}}{1-\overline{p}q+\overline{q}r-r\overline{p}}&-1\end{bmatrix}=\begin{bmatrix}1&-s\\ \overline{s}&-1\end{bmatrix}$

which is clearly a matrix of reversion through point $\displaystyle s=\frac{p-q+r-p\overline{q}r}{1-\overline{p}q+\overline{q}r-r\overline{p}}.\;$ It remains to verify that $s\;$ is collinear with $p,\;$ $q\;$ and $r.\;$

The line of $p,q,r\;$ crosses $\omega\;$ in two points, say $A\;$ and $B\;$ such that $\pi (A)=B,\;$ $\kappa\pi (A)=A,\;$ $\rho\kappa\pi (A)=B,\;$ implying that $\sigma (A)=B,\;$ i.e., that $s\;$ lies on $AB.$

In case where the line of $p,q,r\;$ does not cross $\omega\;$ it is not difficult to verify that, say, $\displaystyle\frac{s-p}{q-r}\in\mathbb{R}.$