Stereographic Projection and Inversion

Hubert Shutrick communicated to me a delightful connection between the stereographic projection and the inversion transform. Inversion is a generalization of a reflection in line. Wonderfully, there is even a more direct connection between inversion and reflection.

The basic configuration consists of a plane and a circle C(O, a) of radius a centered at the origin O. This is the circle of inversion. Inversion is a 1-1 mapping of the plane onto itself (excluding the center of inversion O). Touching the plane at O, there is a sphere S(C, a/2) of diameter a with N as its top point. The points on the sphere are projected to the plane from N. The stereographic projection is a 1-1 mapping between the sphere (excluding the point of projection N) and the xy-plane.

The diagram below shows a cross-section of the configuration by the xz-plane (y = 0). Since both inversion and stereographic projection do not depend on the coordinate system, the particular choice of the coordinates in no way restricts the generality of the argument.

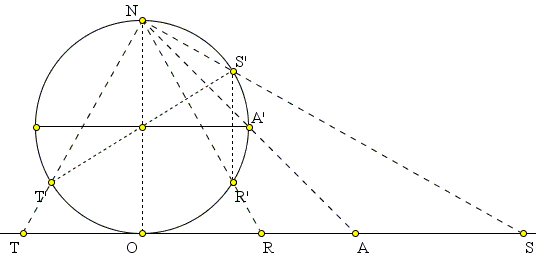
The diagram shows several points: O(0, 0, 0), N(0, 0, a), S(s, 0, 0), R(r, 0, 0), T(-r, 0, 0), A(a, 0, 0). A, R, S, and T are (stereographic) projections of A', R', S', and T', respectively.

The main result of this page is the observation that two points R and S are the inversive images of each other in C(O, a) if and only if their sphere counterparts R' and S' are reflections of each other in the equatorial plane z = a/2.

Proof

Assume R and S are inversive images of each other: rs = a², implying the proportion r / a = a / s in right triangles NOT and SON. Since the sides of the two right triangles are in proportion, the triangles are similar, so that the angles ONT and ONS are complementary. From this ∠SNT = 90° as is ∠S'NT'. Thus S'T' is a diameter of the sphere and T' is the reflection of S' in its center C. We thus have CR' = CT' = CS' so that R' and S' are at the same distance from C and the plane z = a/2 and have the same x (and y) coordinates. Hence, they are reflections of each other in the equatorial plane, as required.

In another direction, assume S' and T' are two antipodal points on the sphere (in xz-plane). Then since ∠S'NT' = 90°, so is ∠SNT, meaning NO² = OT×OS. This shows that S and T are the images of each other under inversion with negative power. If R' is the reflection of T' in NO, then it is also the reflection of S' in the equatorial plane. Its stereographic image R relates to S by the inversion in C(O, a).

There is also an algebraic derivation. Pick point S' = (u, 0, v) on the sphere and find its stereographic projection S.

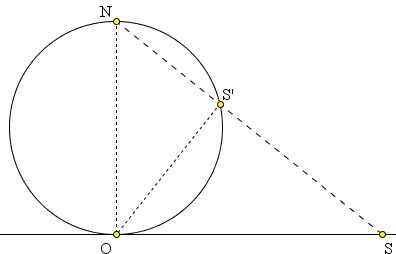
Since NO is the diameter of the sphere (and also of the shown circle) angles OS'N and SON are both right, making triangles OS'N and SS'O right and similar. From their similarity we obtain the proportion:

from which OS = NO · OS' / NS'. We easily find

This gives a formula for expressing stereographic projection in a coordinate form:

Two points S'(u, y, v) and R'(w, y, z) on the sphere are reflections in the equatorial plane if and only if u = w and z = a - v. This shows that, for the projection R(r, 0, 0) of R'(u, 0, a - v), we have

Multiplying the two gives rs = a².

Both inversion and stereographic projection preserve angles and map (generalized, i.e., including straight lines) circles on (generalized) circles. The revealed connection between the two transformations sheds additional light on why this is so. It is also noteworthy that the circles or lines that are orthogonal to the circle of inversion invert to themselves and are images of the vertical circles under stereographic projection.

Finally, there are at least two popular configurations that fall under the rubric of stereographic projection. The one, as above, has a sphere standing on a plane. In the other, the plane cuts through the center of the sphere so that the 2D and 3D coordinate systems share the origin. In the latter, the asserted property holds even more obviously with the circle of inversion being the equatorial circle of the sphere. Among other things, it is immediately obvious that as the reflection in the equatorial plane exchanges the upper and lower semispheres so the inversion exchanges the interior of the circle of inversion with its exterior.

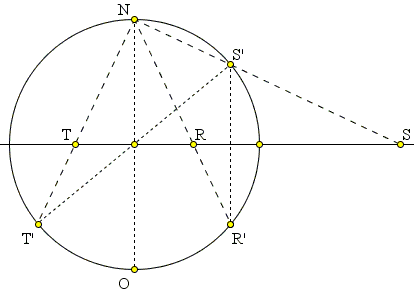
The algebraic derivation is even simpler. For S'(u, 0, v), u² + v² = a², s = au / (a - v). For its reflection R'(u, 0, -v), r = au / (a + v). Therefore,

Note: Stereographic projection serves an enlightening model for another geometric construct, the radical axis of two circles.

2D Problems That Benefit from a 3D Outlook

1. Four Travellers, Solution
2. Desargues' Theorem
3. Soddy Circles and Eppstein's Points
4. Symmetries in a Triangle
5. Three Circles and Common Chords
6. Three Circles and Common Tangents
7. Three Equal Circles
8. Menelaus from 3D
9. Stereographic Projection and Inversion
10. Stereographic Projection and Radical Axes
11. Sum of Squares in Equilateral Triangle

Stereographic Projection

• Stereographic Projection and Radical Axes
• Stereographic Projection and Inversion
• Stereographic Projection of a Coffin Problem
• Stereographic Projection - an Interactive Tool
• Objects distant and near

Inversion - Introduction

• Angle Preservation Property
• Apollonian Circles Theorem
• Archimedes' Twin Circles and a Brother
• Bisectal Circle
• Chain of Inscribed Circles
• Circle Inscribed in a Circular Segment
• Circle Inversion: Reflection in a Circle
• Circle Inversion Tool
• Feuerbach's Theorem: a Proof
• Four Touching Circles
• Hart's Inversor
• Inversion in the Incircle
• Inversion with a Negative Power
• Miquel's Theorem for Circles
• Peaucellier Linkage
• Polar Circle
• Poles and Polars
• Ptolemy by Inversion
• Radical Axis of Circles Inscribed in a Circular Segment
• Steiner's porism
• Stereographic Projection and Inversion
• Tangent Circles and an Isosceles Triangle
• Tangent Circles and an Isosceles Triangle II
• Three Tangents, Three Secants
• Viviani by Inversion
• Simultaneous Diameters in Concurrent Circles

Radical Axis and Radical Center

• A Property of the Line IO: A Proof From The Book
• Cherchez le quadrilatere cyclique II
• Circles On Cevians
• Circles And Parallels
• Circles through the Orthocenter
• Coaxal Circles Theorem
• Isosceles on the Sides of a Triangle
• Properties of the Circle of Similitude
• Six Concyclic Points
• Radical Axis and Center, an Application
• Radical axis of two circles
• Radical Axis of Circles Inscribed in a Circular Segment
• Radical Center
• Radical center of three circles
• Steiner's porism
• Stereographic Projection and Inversion
• Stereographic Projection and Radical Axes
• Tangent as a Radical Axis
• Two Circles on a Side of a Triangle
• Pinning Butterfly on Radical Axes
• Two Lines - Two Circles
• Two Triples of Concurrent Circles
• Circle Centers on Radical Axes
• Collinearity with the Orthocenter

|Contact| |Front page| |Contents| |Geometry| |Store|