Butterfly in Complex Numbers
Albrecht Hess
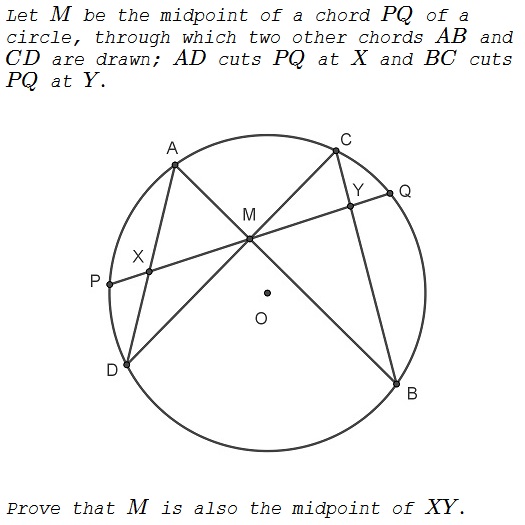
Proof
Let $A, B, C, D$ be points on the unit circle and $M$ the intersection of $AB$ and $CD$.The equation of the points $Z$ on the secant line through $A$ and $B$ is
$z+ab\,\overline{z}=a+b.$
The lowercase letters refer to the complex numbers representing the corresponding points.Since $M$ is a point of $AB$ and $CD$ we have
$\displaystyle b=\frac{m-a}{1-a\,\overline{m}}$
and
$\displaystyle d=\frac{m-c}{1-c\,\overline{m}}.$
Let the secant $PQ$ be orthogonal to $OM$, hence tangent to the circle around $O$ through $M$. For a point $Z$ an $PQ$ we have therefore the equation
$z\,\overline{m}+\overline{z}\,m=2m\overline{m}.$
The intersection $X$ of $PQ$ and $AD$ can be obtained as a common solution of the equation of $PQ$ and the equation $z+ad\overline{z}=a+d$ of the secant line throught $A$ and $D$
$\displaystyle x=\frac{a\,m+d\,m-2ad\,m\overline{m}}{m-ad\,\overline{m}}.$
Insert the expression for $d$ from above and write $x$ as
$\displaystyle x=\frac{m(-a+c-m-ac\,\overline{m}+2a\,m\overline{m})} {-m-ac\,\overline{m}+a\,m\overline{m}+c\,m\overline{m}}.$
By the same argument, but inserting the expression for $b$ , we get for the intersection $Y$ of $PQ$ and $BC$ simply by interchanging $a$ and $c$
$\displaystyle y=\frac{m(-c+a-m-ac\,\overline{m}+2c\,m\overline{m})} {-m-ac\,\overline{m}+a\,m\overline{m}+c\,m\overline{m}}.$
The sum of $x$ and $y$ is indeed $2m$ and $M$ is the midpoint of $XY$.
![]()
Butterfly Theorem and Variants
- Butterfly theorem
- 2N-Wing Butterfly Theorem
- Better Butterfly Theorem
- Butterflies in Ellipse
- Butterflies in Hyperbola
- Butterflies in Quadrilaterals and Elsewhere
- Pinning Butterfly on Radical Axes
- Shearing Butterflies in Quadrilaterals
- The Plain Butterfly Theorem
- Two Butterflies Theorem
- Two Butterflies Theorem II
- Two Butterflies Theorem III
- Algebraic proof of the theorem of butterflies in quadrilaterals
- William Wallace's Proof of the Butterfly Theorem
- Butterfly theorem, a Projective Proof
- Areal Butterflies
- Butterflies in Similar Co-axial Conics
- Butterfly Trigonometry
- Butterfly in Kite
- Butterfly with Menelaus
- William Wallace's 1803 Statement of the Butterfly Theorem
- Butterfly in Inscriptible Quadrilateral
- Camouflaged Butterfly
- General Butterfly in Pictures
- Butterfly via Ceva
- Butterfly via the Scale Factor of the Wings
- Butterfly by Midline
- Stathis Koutras' Butterfly
- The Lepidoptera of the Circles
- The Lepidoptera of the Quadrilateral
- The Lepidoptera of the Quadrilateral II
- The Lepidoptera of the Triangle
- Two Butterflies Theorem as a Porism of Cyclic Quadrilaterals
- Two Butterfly Theorems by Sidney Kung
- Butterfly in Complex Numbers
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73601937
