A Better Butterfly Theorem

The following generalization of the Butterfly Problem has been pointed out to me by Qiu Fawen, a Chinese teacher who discovered the result with his students in 1997. The Chinese version was at some time available at qiusir.com. I had to do some guess work to figure out what it was about.

According to Leon Bankoff (Mathematics Magazine, Volume 60, No. 4, October 1987, pp. 195-210) the appellation The Butterfly made its first appearance in the Solutions section of the American Mathematical Monthly in the February 1944 issue. Since the diagram of the theorem (with two wings on each side) established by Qiu Fawen and his students gives a more realistic depiction of a butterfly, I suggest to call the statement A Better Butterfly Theorem which might be interpreted as both A "Better Butterfly" Theorem and A Better "Butterfly Theorem", the former being my preference.

A Better Butterfly Theorem

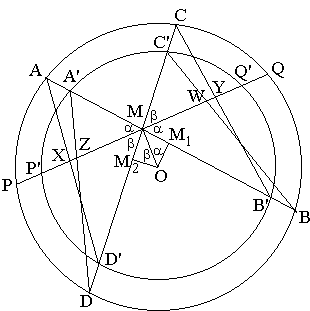
Let there be two concentric circles with the common center O. A line crosses the two circles at points P, Q and P', Q', M being the common midpoint of PQ and P'Q'. Through M, draw two lines AA'B'B and CC'D'D and connect AD', A'D, BC', and B'C. (This is the Butterfly.) Let X, Y, Z, W be the points of intersection of PP'Q'Q with AD', B'C, A'D, and BC', respectively. Then

(1)	1/MX + 1/MZ = 1/MY + 1/MW.

(Since X coincides with Z and Y with W when the two circles coalesce into one, The Butterfly Theorem is an immediate consequence of A Better Butterfly Theorem.)

The proof depends on the following

Lemma

Let in ΔRST, RU be a cevian through vertex R. Introduce angles a = ∠SRU and b = ∠URT. Then

(2)	sin(a + b)/RU = sin(a)/RT + sin(b)/RS.

The proof follows from the fact that Area( ΔRST) = Area( ΔRSU) + Area( ΔRUT) by a consistent application of the sine formula for the area of a triangle. (For example, Area( ΔRST) = RS·RT·sin(a + b)/2.)

Proof of the theorem

We apply Lemma to triangles AMD', A'MD, B'MC, and BMC':

(3)	sin(a + b)/MX = sin(a)/MD' + sin(b)/MA, sin(a + b)/MZ = sin(a)/MD + sin(b)/MA', sin(a + b)/MY = sin(a)/MC + sin(b)/MB', sin(a + b)/MW = sin(a)/MC' + sin(b)/MB.

In view of (3), (1) will follow from

(4)	sin(a)/MD' + sin(b)/MA + sin(a)/MD + sin(b)/MA' = sin(a)/MC + sin(b)/MB' + sin(a)/MC' + sin(b)/MB,

or, which is the same, from

(5)	sin(b)(1/MA - 1/MB) + sin(b)(1/MA' - 1/MB') = sin(a)(1/MC - 1/MD) + sin(a)(1/MC' - 1/MD').

Now, drop perpendiculars OM₁ and OM₂ from O onto AA'B'B and CC'D'D. M₁ is the midpoint of both AB and A'B', whereas M₂ is the midpoint of CD and C'D'. Obviously,

(6)	MB - MA = MB' - MA' = 2·OM₁ = 2·OM·sin(a) and MD - MC = MD' - MC' = 2·OM₂ = 2·OM·sin(b).

With (6) in mind, (5) is equivalent to

(7)	1/MA·MB + 1/MA'·MB' = 1/MC·MD + 1/MC'·MD'.

However, as is well known, MA·MB = MC·MD and MA'·MB' = MC'·MD'. Therefore, (7) is true, as is (5), which in turn, implies (1).

Butterfly Theorem and Variants

71867351