The Lepidoptera of the Triangle
Sidney Kung
July, 2107
Theorem 1
Proof of Theorem 1
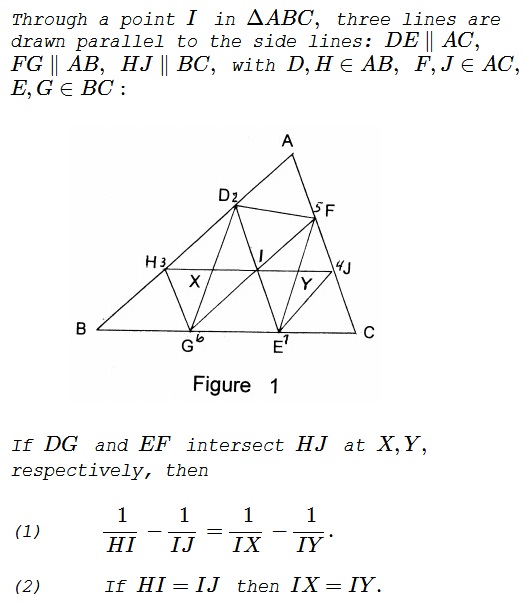
We begin by assuming a more general case than that shown in Figure 1, in that
- none of the three transversals $DE\,$ $FG,\,$ and $HJ\,$ needs to be parallel to a side of $\Delta ABC,$
- we only ask that the points $P=AB\cap FG,\,$ $Q=HJ\cap BC,\,$ $R=DE\cap AC\,$ be collinear.
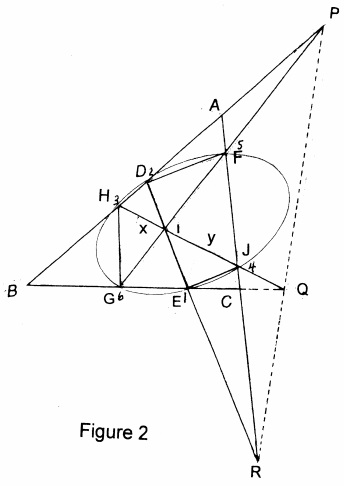
Denote the six vertices of the hexagon $HDFJEG\,$ in the order $325416.\,$ We see that the points of intersections of the three pairs of the opposite sides $23-56,\,$ $34-61,\,$ $12-45\,$ are, respectively $P,\,$ $Q,\,$ $R.\,$ Thus, by the converse of Pascal's Theorem, if $P,\,$ $Q,\,$ $R\,$ are collinear, the hexagon $HDFJEG\,$ is inscribed in a conic.
Return to Figure 1. Denote the vertices of the hexagon $HDFJEG\,$ in the order $325416.\,$ Since $FG\parallel AB,\,$ $23-56\,$ meet at a point of infinity. Similarly, the same holds for $34-61\,$ and $12-45.\,$ Thus, the points $P,\,$ $Q,\,$ $R,\,$ all being points at infinity, are collinear, hence the hexagon $HDFJEG\,$ is inscribed in a conic. It follows then from Candy's generalized Butterfly Theorem, that
$\displaystyle \frac{1}{HI}-\frac{1}{IJ}=\frac{1}{IX}-\frac{1}{IY},$
which is (1), and (2) is immediate if $I\,$ is the midpoint of $HJ.$
Theorem 2
With a reference to Figure 3i, three lines $DE,\,$ $FG,\,$ $HJ\,$ are drawn through point $I\\,$ in $\Delta ABC,\,$ tangent to the circumcircles $(AIC),\,$ $(BIA)\,$ $(BIC),\,$ respectively.
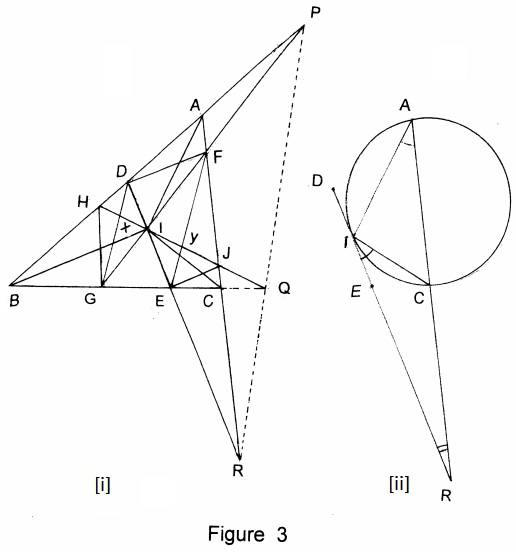
Let $P=AB\cap FG,\,$ $Q=HJ\cap BC,\,$ $R=DE\cap AC.\,$ If $DG\,$ and $EF\,$ intersect $HJ\,$ at $X,Y,\,$ respectively, then
(3)
$\displaystyle \frac{1}{HI}-\frac{1}{IJ}=\frac{1}{IX}-\frac{1}{IY}.$
(4)
If $HI=IJ\,$ then $IX=IY.$
Proof of Theorem 2
Consider $DR\,$ and the circumscribe circle of $\Delta AIC$ (see Figure 3ii). It's easy to see that $\Delta RIA\sim\Delta RCI.\,$ So,
$\displaystyle \frac{RA}{RI}=\frac{IA}{IC},\;\frac{RC}{RI}=\frac{AC}{IA}.$
Dividing the former by the latter, we get $\displaystyle \frac{RA}{RI}=\frac{IA^2}{IC^2}.\,$ Similarly, since $\Delta HQC\sim\Delta QBI\,$ and $\Delta PIC\sim\Delta PBI,\,$ $\displaystyle \frac{QC}{QB}=\frac{IC^2}{IB^2}\,$ and $\displaystyle \frac{PB}{PA}=\frac{IB^2}{IA^2}.\,$ Thus
$\displaystyle \frac{PB}{PA}\cdot\frac{QC}{QB}\cdot\frac{RA}{RC}=\frac{IB^2}{IA^2}\cdot\frac{IC^2}{IB^2}\cdot\frac{IA^2}{IC^2}=1.$
By the converse of Menelaus' theorem, the three points $P,Q,R\,$ are collinear, implying that the hexagon $HDFJEG\,$ is inscribed in a conic. Consequently, Candy's theorem delivers (3) and (4).
Butterfly Theorem and Variants
- Butterfly theorem
- 2N-Wing Butterfly Theorem
- Better Butterfly Theorem
- Butterflies in Ellipse
- Butterflies in Hyperbola
- Butterflies in Quadrilaterals and Elsewhere
- Pinning Butterfly on Radical Axes
- Shearing Butterflies in Quadrilaterals
- The Plain Butterfly Theorem
- Two Butterflies Theorem
- Two Butterflies Theorem II
- Two Butterflies Theorem III
- Algebraic proof of the theorem of butterflies in quadrilaterals
- William Wallace's Proof of the Butterfly Theorem
- Butterfly theorem, a Projective Proof
- Areal Butterflies
- Butterflies in Similar Co-axial Conics
- Butterfly Trigonometry
- Butterfly in Kite
- Butterfly with Menelaus
- William Wallace's 1803 Statement of the Butterfly Theorem
- Butterfly in Inscriptible Quadrilateral
- Camouflaged Butterfly
- General Butterfly in Pictures
- Butterfly via Ceva
- Butterfly via the Scale Factor of the Wings
- Butterfly by Midline
- Stathis Koutras' Butterfly
- The Lepidoptera of the Circles
- The Lepidoptera of the Quadrilateral
- The Lepidoptera of the Quadrilateral II
- The Lepidoptera of the Triangle
- Two Butterflies Theorem as a Porism of Cyclic Quadrilaterals
- Two Butterfly Theorems by Sidney Kung
- Butterfly in Complex Numbers
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73599961
