Areal Butterflies

Sidney Kung
May 14, 2012

Circles \(O_1\) and \(O_2\) intersect in points \(M\) and \(N\). Line passing through \(M\) intersect\(O_1\) and \(O_2\) in \(A\) and \(B\), respectively. Line passing through \(N\) intersect\(O_1\) and \(O_2\) in \(C\) and \(D\), respectively. If \(AB\) does not intersect \(CD\), and if \(AD\cap BC=I\), then \([\Delta AIB]=[\Delta CID]\), where, \([\Omega ]\) indicates the area of figure \(\Omega\).

Proof

|Contact| |Front page| |Contents| |Geometry| |Store|

Circles \(O_1\) and \(O_2\) intersect in points \(M\) and \(N\). Line passing through \(M\) intersect\(O_1\) and \(O_2\) in \(A\) and \(B\), respectively. Line passing through \(N\) intersect\(O_1\) and \(O_2\) in \(C\) and \(D\), respectively. If \(AB\) does not intersect \(CD\), and if \(AD\cap BC=I\), then \([\Delta AIB]=[\Delta CID]\), where, \([\Omega ]\) indicates the area of figure \(\Omega\).

Proof

There are two cases to consider:

		\(A,M,N,C\in O_{1},\space \alpha +\gamma = \pi\) \(B,M,N,D \in O_{2},\space \gamma = \beta\) Therefore, \(\alpha + \beta = \pi\) \(\Rightarrow \space AC||BD\) \(\Rightarrow \space [\Delta ACB]=[\Delta CAD]\) \(\Rightarrow \space [\Delta AIB]=[\Delta CID]\).
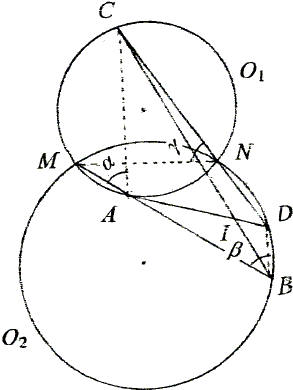		\(A,M,N,C\in O_{1},\space \alpha = \gamma\) \(B,M,N,D \in O_{2},\space \gamma = \beta\) Therefore, \(\alpha = \beta\) \(\Rightarrow \space AC||BD\) \(\Rightarrow \space [\Delta BDA]=[\Delta BDC]\) \(\Rightarrow \space [\Delta AIB]=[\Delta CID]\).

Butterfly Theorem and Variants

1. Butterfly theorem
2. 2N-Wing Butterfly Theorem
3. Better Butterfly Theorem
4. The Lepidoptera of the Circles
5. The Lepidoptera of the Quadrilateral
6. The Lepidoptera of the Quadrilateral II
7. Butterflies in Ellipse
8. Butterflies in Hyperbola
9. Butterflies in Quadrilaterals and Elsewhere
10. Pinning Butterfly on Radical Axes
11. Shearing Butterflies in Quadrilaterals
12. The Plain Butterfly Theorem
13. Two Butterflies Theorem
14. Two Butterflies Theorem II
15. Two Butterflies Theorem III
16. Algebraic proof of the theorem of butterflies in quadrilaterals
17. William Wallace's Proof of the Butterfly Theorem
18. Butterfly theorem, a Projective Proof
19. Areal Butterflies
20. Butterflies in Similar Co-axial Conics
21. Butterfly Trigonometry
22. Butterfly in Kite
23. Butterfly with Menelaus
24. William Wallace's 1803 Statement of the Butterfly Theorem
25. Butterfly in Inscriptible Quadrilateral

|Contact| |Front page| |Contents| |Geometry| |Store|