Circle Centers on Radical Axes
What is this about?
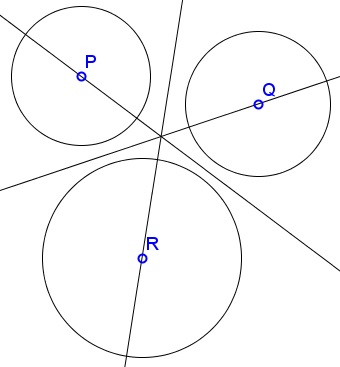
A Mathematical Droodle
(Three circles. Drag by any boundary point. Change radius by dragging the center.)
|Activities| |Contact| |Front page| |Contents| |Geometry| |Generalization|
Copyright © 1996-2018 Alexander Bogomolny
The applet attempts to suggest the following statement:
Let there be three circles (P), (Q), (R) centered at P, Q, and R, respectively. Assume that P lies on the radical axes of (Q) and (R); Q, on that of (P) and (R). Then R lies on the radical axis of (P) and (Q).
Proof
The radical axis of two circles is perpendicular to their centerline. Let's denote the radical axes of circles centered at points U and V as LUV.
If, as stipulated in the problem, P lies LQR and Q lies on LPR, then the two lines serve as altitudes (from P and Q) of ΔPQR. Their intersection - the radical center O of (P), (Q), (R) - doubles as the orthocenter of the triangle. The third altitude (from R) is perpendicular to PQ and passes through the radical center O, but there is only one perpendicular to PQ through O and this is the radical axis LPQ. It follows that R ∈
Note: this problem generalizes another one where the three circle have been assume to be concurrent. The proof is only a slight modification of one of the proofs of the latter.
Radical Axis and Radical Center
- How to Construct a Radical Axis
- A Property of the Line IO: A Proof From The Book
- Cherchez le quadrilatere cyclique II
- Circles On Cevians
- Circles And Parallels
- Circles through the Orthocenter
- Coaxal Circles Theorem
- Isosceles on the Sides of a Triangle
- Properties of the Circle of Similitude
- Six Concyclic Points
- Radical Axis and Center, an Application
- Radical axis of two circles
- Radical Axis of Circles Inscribed in a Circular Segment
- Radical Center
- Radical center of three circles
- Steiner's porism
- Stereographic Projection and Inversion
- Stereographic Projection and Radical Axes
- Tangent as a Radical Axis
- Two Circles on a Side of a Triangle
- Pinning Butterfly on Radical Axes
- Two Lines - Two Circles
- Two Triples of Concurrent Circles
- Circle Centers on Radical Axes
- Collinearity with the Orthocenter
- Six Circles with Concurrent Pairwise Radical Axes
- Six Concyclic Points on Sides of a Triangle
- Line Through a Center of Similarity
|Activities| |Contact| |Front page| |Contents| |Geometry| |Generalization|
Copyright © 1996-2018 Alexander Bogomolny
73609241
