Generalization of Butterfly's Theorem

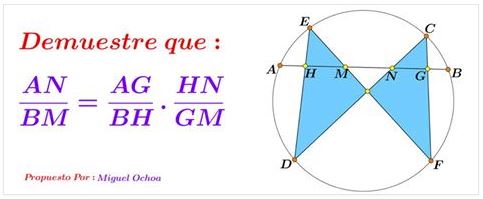
Part 1

Using Hiroshi Haruki's Lemma

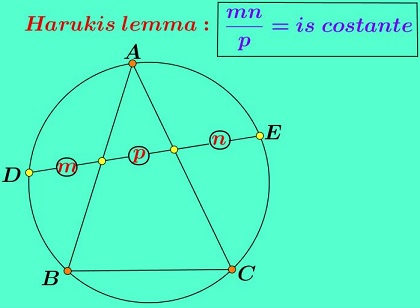
Part 2

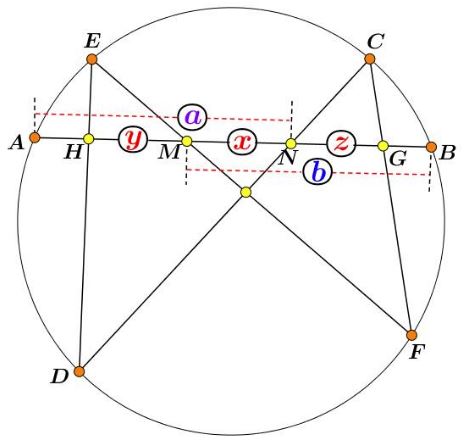
Remark

Assuming $a=b,\,$ the main result becomes $(a+z)(y+x)=(b+y)(z+x)\,$ which reduces to $(a-x)(y-z)=0,\,$ and, since $a\ne x,\,$ $y=z,\,$ proving the Butterfly theorem.

Butterfly Theorem and Variants

1. Butterfly theorem
2. 2N-Wing Butterfly Theorem
3. Better Butterfly Theorem
4. Butterflies in Ellipse
5. Butterflies in Hyperbola
6. Butterflies in Quadrilaterals and Elsewhere
7. Pinning Butterfly on Radical Axes
8. Shearing Butterflies in Quadrilaterals
9. The Plain Butterfly Theorem
10. Two Butterflies Theorem
11. Two Butterflies Theorem II
12. Two Butterflies Theorem III
13. Algebraic proof of the theorem of butterflies in quadrilaterals
14. William Wallace's Proof of the Butterfly Theorem
15. Butterfly theorem, a Projective Proof
16. Areal Butterflies
17. Butterflies in Similar Co-axial Conics
18. Butterfly Trigonometry
19. Butterfly in Kite
20. Butterfly with Menelaus
21. William Wallace's 1803 Statement of the Butterfly Theorem
22. Butterfly in Inscriptible Quadrilateral
23. Camouflaged Butterfly
24. General Butterfly in Pictures
25. Butterfly via Ceva
26. Butterfly via the Scale Factor of the Wings
27. Butterfly by Midline
28. Stathis Koutras' Butterfly
29. The Lepidoptera of the Circles
30. The Lepidoptera of the Quadrilateral
31. The Lepidoptera of the Quadrilateral II
32. The Lepidoptera of the Triangle
33. Two Butterflies Theorem as a Porism of Cyclic Quadrilaterals
34. Two Butterfly Theorems by Sidney Kung
35. Butterfly in Complex Numbers

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny