Six Circles with Concurrent Pairwise Radical Axes
Problem
To construct six non-concurrent not all equal circles such that the radical axes of all pairs of the circles are concurrent.

Construction
Let $ABC$ be a triangle and $AA',$ $BB',$ $CC'$ its internal angle bisectors. Let $A_b$ be the orthogonal projection of $A$ on $BB'.$ (Similarly define projections from other vertices onto other angle bisectors.) One circle is the circle $(A_{b})=(A_{b}, A_{b}A),$ i.e., the circle with center $A_b$ and radius $A_{b}A.$ Similarly, the circle $(A_{c})=(A_{c}, A_{c}A)$ where $A_c$ is the orthogonal projection of $A$ on $CC'.$ The remaining 4 circles are defined in analogous manner.
The radical axis of any pair of these circles passes through the orthocenter of $\Delta ABC.$
Hint
Circle $(A_{b})$ passes through, say $H_a$ - the foot of the $A$-altitude of $\Delta ABC.$ Indeed, $(A_{b})$ crosses $BC$ in two points. One, say, $A''$ is the end of the diameter $AA''.$ The other forms the right angle with legs through $A$ and $A''$ which surely defines $H_a.$
Proof for circles $(A_b)$ and $(A_c)$
Both $(A_b)$ and $(A_c)$ path through $A$ and $H_a,$ implying that $AH_a$ is their radical axis. This is the $A$-altitude of $\Delta ABC$ and, thus, passes through its orthocenter.
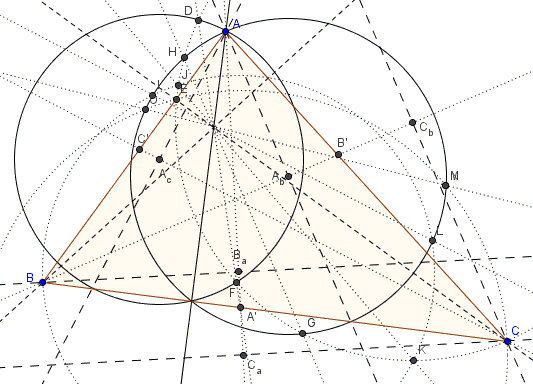
Proof for circles $(A_b)$ and $(B_a)$
Draw circle $(C')$ with $AB$ as diameter. $AH_a$ is the radical axis of $(C')$ and $(A_b),$ while $(BH_b)$ is the radical axis of $(C')$ and $(B_a).$ The two meet at the orthocenter of $\Delta ABC,$ meaning that the latter serves the radical center of the three circles. Therefore, the radical axis of the third pair, $(A_b)$ and $(B_a),$ also passes through that point.

Proof for circles $(A_b)$ and $(C_a)$

With a change of indices and vertices, it was already shown that the radical axis of $(A_b)$ and $(A_c)$ (Case #1) and that of $(A_c)$ and $(C_a)$ (Case #2) both pass through the orthocenter of $\Delta ABC$ and so does the radical axis of the third pair, $(A_b)$ and $(C_a).$
Proof for circles $(A_b)$ and $(C_b)$
Same as the previous case.
Acknowledgment
The problem and the construction have been posted by $\alpha\nu\tau\rho\epsilon\alpha\varsigma\space\chi\alpha\tau\zeta\eta\pi o\lambda\alpha\kappa\eta\varsigma\space$ at the CutTheKnotMath facebook page. He also observed that there is a simple case where the six circles are allowed to be congruent. If they are, the simple solution is to place the circles at the vertices of a regular hexagon.
Radical Axis and Radical Center
- How to Construct a Radical Axis
- A Property of the Line IO: A Proof From The Book
- Cherchez le quadrilatere cyclique II
- Circles On Cevians
- Circles And Parallels
- Circles through the Orthocenter
- Coaxal Circles Theorem
- Isosceles on the Sides of a Triangle
- Properties of the Circle of Similitude
- Six Concyclic Points
- Radical Axis and Center, an Application
- Radical axis of two circles
- Radical Axis of Circles Inscribed in a Circular Segment
- Radical Center
- Radical center of three circles
- Steiner's porism
- Stereographic Projection and Inversion
- Stereographic Projection and Radical Axes
- Tangent as a Radical Axis
- Two Circles on a Side of a Triangle
- Pinning Butterfly on Radical Axes
- Two Lines - Two Circles
- Two Triples of Concurrent Circles
- Circle Centers on Radical Axes
- Collinearity with the Orthocenter
- Six Circles with Concurrent Pairwise Radical Axes
- Six Concyclic Points on Sides of a Triangle
- Line Through a Center of Similarity
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73561970
