The Lepidoptera of the Quadrilateral II
Sidney Kung
April 26, 2008
We prove the Butterfly Theorem with the aid of Menelaus' theorem.
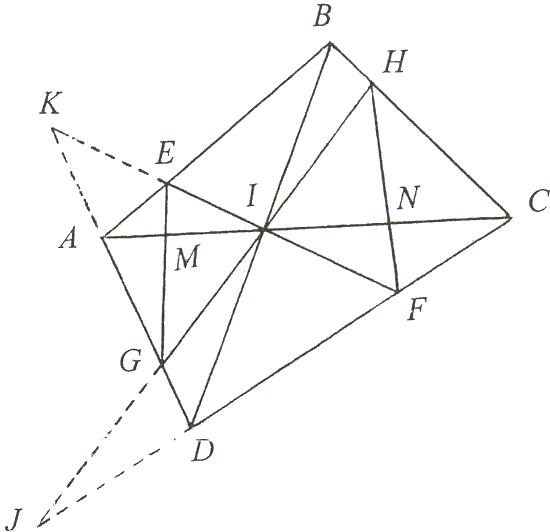
Through the intersection I of the diagonals AC, BD of a convex quadrilateral ABCD, draw two lines EF and HG that meet the sides of ABCD in E, F, G, H. Let M and N be the intersections of EG and FH with AC. Then
| |
1/IM - 1/IA = 1/IN - 1/IC.
|
Proof
| |  |
| | Figure 1. |
Refer to Figure 1. Triangles BAD and CAD are cut by transversal EIF. So, by applying Menelaus' theorem twice, we have
| |
BE/EA · AK/KD · DI/IB = 1,
CF/FD · DK/KA · AI/IC = 1.
|
Multiplying the above gives
| |
BE/EA · ID/IB · CF/FD · IA/IC = 1,
|
or
| (1) |
IA · ID · BE/EA = IC · IB · FD/CF.
|
Similarly, since transversal HIG cuts triangles BDC and ADC, applying Menelaus' theorem twice again will give us
| |
AG/GD · DI/IB · BH/HC · CI/IA = 1,
|
or
| (2) |
ID · IC · BH/HC = IB · IA · DG/GA.
|
Note that neither (1) nor (2) involves IM, MA, IN, or NC. The relationship among these and other line segments in the figure will be established as follows:
| |  |
| | Figure 2. |
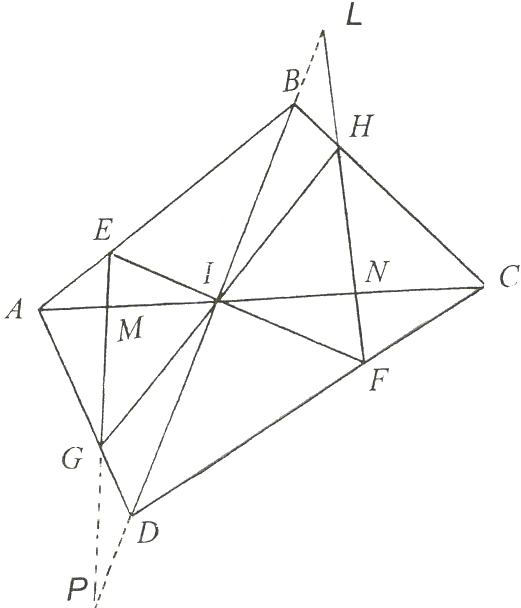
Refer to Figure 2. Let L and P be the intersections of FH and EG with BG. Consider the triangle CDI with transversal FH, we have
| |
DF/ FC · CN/NI · IL/LD =1,
|
or
| (3) |
DF/FC = IN/NC · LD/IL.
|
Similarly, from triangle CIB, we see that
| |
BH/HC · CN/NI · IL/LB = 1,
|
or
| (4) |
BH/HC = NI/CN · LB/IL.
|
Thus,
| (5) |
| IB · DF/ FC + DI · BH/HC | = IB · IN/NC · LD/IL + DI · NI/CN · LB / IL |
| | = NI/CN · (IB · ID + DI · LB) / IL |
| | = NI/CN · (IB · (DI + IL) + DI · (IL- IB)) / IL |
| | = DB · IN/NC. |
|
Again, we apply the Menelaus theorem on triangles AIB and ADI to get
| (6) |
BE/EA = MI / AM · PB/IP
|
and
| (7) |
DG / GA = MI / AM · PD/IP,
|
respectively. So,
| (8) |
| IB · DG/GA + ID · BE / EA | = MI/MA (IB · PD + PB · ID) / IP |
| | = MI/MA · (BI · (IP - ID) + ID · (PI + IB)) / IP |
| | = BD · IM/MA. |
|
Now, multiplying (5) by IC, we get
| (9) |
IC · IB · DF/FC + IC · ID · BH/HC = IC · BD · IN/NC
|
and multiply (8) by IA, we have
| (10) |
IA · IB · DG/GA + IA · ID · BE/EA = IA · BD · IM/MA.
|
Finally, by subtracting (10) from (9), and taking into account (1) and (2), we obtain
| |
BD · ((IC · IN)/NC - (IA · IM)/MA ) = 0.
|
It follows then that
| |
(IA - IM)/(IA · IM) = (IC - IN) / (IC · IN).
|
Therefore, 1/IM - 1/IA = 1/IN - 1/IC, as required
Butterfly Theorem and Variants
- Butterfly theorem
- 2N-Wing Butterfly Theorem
- Better Butterfly Theorem
- The Lepidoptera of the Circles
- The Lepidoptera of the Quadrilateral
- The Lepidoptera of the Quadrilateral II
- Butterflies in Ellipse
- Butterflies in Hyperbola
- Butterflies in Quadrilaterals and Elsewhere
- Pinning Butterfly on Radical Axes
- Shearing Butterflies in Quadrilaterals
- Two Butterflies Theorem
- Two Butterflies Theorem II
- Two Butterflies Theorem III
Copyright © 1996-2009 Alexander Bogomolny
|
