Four Hinged Squares

The purpose of the applet below is to illustrate an 1826 sangaku hung by Ikeda Sadakazu in an Azabu shrine, Tokyo. The tablet since disappeared but not before it was recorded in an 1827 book Shamei Sanpu (Sacred Mathematics) by Shiraishi Nagatada (1795-1862). The problem has also been included in an 1840 collection Sanpo Chokujutsu Seikai (Mathematics without Proof) by Heinouchi Masaomi.

I first stumbled upon this simple problem in the Temple Geometry by Fukagawa and Pedoe, where it was listed without solution. My solution that employs Bottema's theorem appears on a separate page. Michel Cabart gave a solution that employed complex numbers. The newer book Sacred Geometry by Fukagawa and Rothman also lists the problem but now with the original solution from Sanpo Chokujutsu Seikai where it read:

Fukagawa and Rothman give a solution nonetheless.

Shamei Sanpu in general contains by far more difficult problems. For example, the page where the four hinged squares is presented also includes a problem of determining the surface area of an ellipsoid:

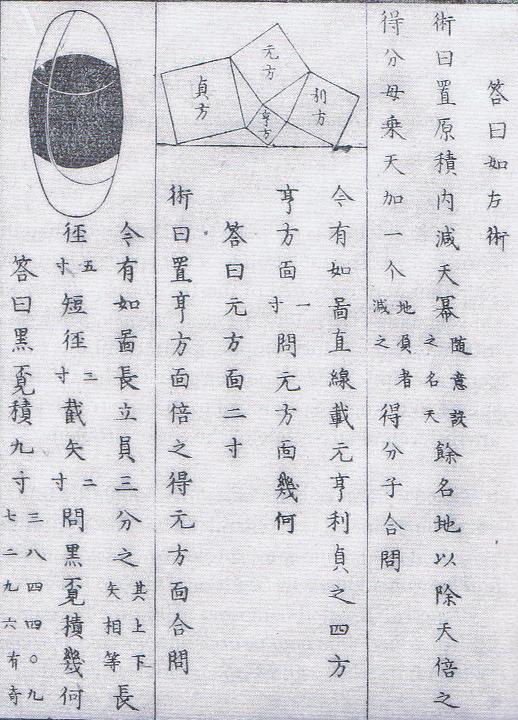
References

1. H. Fukagawa, D. Pedoe, Japanese Temple Geometry Problems, The Charles Babbage Research Center, Winnipeg, 1989

   Write to:

   Charles Babbage Research Center
   P.O. Box 272, St. Norbert Postal Station
   Winnipeg, MB
   Canada R3V 1L6

2. H. Fukagawa, A. Rothman, Sacred Geometry: Japanese Temple Geometry, Princeton University Press, 2008, p. 149

Copyright © 1996-2009 Alexander Bogomolny

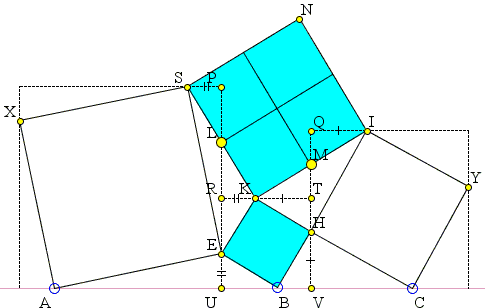
Square BEKH is inscribed in square UVTR so that

HV = KT

(and also EU = KR.) In the square circumscribing square CYIH,

HV = IQ

implying KT = IQ. Let M be the intersection of QT and IK. Then triangles KTM and IQM are congruent so that M is the midpoint of IK (KM = IM). Similarly, on the other side, KL = SL.

We conclude that since KM = KL and angle LKM is right while angle RKT is straight, triangles LRK and KTM are congruent. In square UVTR, KR = HT. So it follows that triangles LRK and KTH are also congruent leading to

Δ KTH = Δ KTM

and KM = KH. Just what was needed.

Incidently, there is another sangaku with a similar configuration:

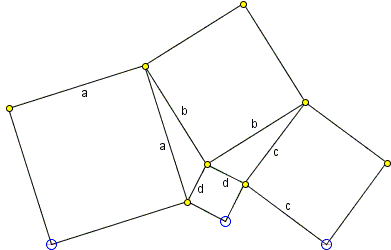
This has been written in 1832 also in the Tokyo prefecture and was recorded in Kokon Sankan by Uchida Gokan [Temple Geometry, p. 131]. The problem is to express d in terms of a, b, c. The solution is more conventional. Apply the Law of Cosines to triangles abd and bcd:

where X is the cosine of the angle between b and d in triangle abd.

Adding the two gives:

from which d is found to be

Sangaku

1. Sangaku: Reflections on the Phenomenon
2. Critique of My View and a Response
3. 1 + 27 = 12 + 16 Sangaku
4. 3-4-5 Triangle by a Kid
5. 7 = 2 + 5 Sangaku
6. A 49^th Degree Challenge
7. A Geometric Mean Sangaku
8. A Hard but Important Sangaku
9. A Restored Sangaku Problem
   • A better solution to a difficult sangaku problem
10. A Sangaku: Two Unrelated Circles
11. A Sangaku by a Teen
12. A Sangaku Follow-Up on an Archimedes' Lemma
13. A Sangaku with an Egyptian Attachment
14. A Sangaku with Many Circles and Some
15. A Sushi Morsel
16. An Old Japanese Theorem
17. Archimedes Twins in the Edo Period
18. Arithmetic Mean Sangaku
19. Bottema Shatters Japan's Seclusion
20. Circles and Semicircles in Rectangle
21. Circles in a Circular Segment
22. Circles Lined on the Legs of a Right Triangle
23. Equal Incircles Theorem
24. Equilateral Triangle, Straight Line and Tangent Circles
25. Equilateral Triangles and Incircles in a Square
26. Five Incircles in a Square
27. Four Hinged Squares
28. Four Incircles in Equilateral Triangle
29. Gion Shrine Problem
30. Harmonic Mean Sangaku
31. Heron's Problem
32. In the Wasan Spirit
33. Incenters in Cyclic Quadrilateral
34. Japanese Art and Mathematics
35. Malfatti's Problem
36. Maximal Properties of the Pythagorean Relation
37. Neuberg Sangaku
38. Out of Pentagon Sangaku
39. Peacock Tail Sangaku
40. Pentagon Proportions Sangaku
41. Pythagoras and Vecten Break Japan's Isolation
42. Radius of a Circle by Paper Folding
43. Review of Sacred Mathematics
44. Sangaku à la V. Thebault
45. Sangaku and The Egyptian Triangle
46. Sangaku in a Square
47. Sangaku Iterations, Is it Wasan?
48. Sangaku with 8 Circles
49. Sangaku with Three Mixtilinear Circles
50. Sangaku with Versines
51. Sangakus with a Mixtilinear Circle
52. Sequences of Touching Circles
53. Square and Circle in a Gothic Cupola
54. Tangent Circles and an Isosceles Triangle
55. The Squinting Eyes Theorem
56. Steiner's Sangaku
57. Three Incircles In a Right Triangle
58. Three Squares and Two Ellipses
59. Three Tangent Circles Sangaku
60. Triangles, Squares and Areas from Temple Geometry
61. Two Arbelos, Two Chains
62. Two Circles in an Angle
63. Two Sangaku with Equal Incircles

Copyright © 1996-2009 Alexander Bogomolny