Four Hinged Squares
The problem of four hinged squares appeared in 1826 as a sangaku hung by Ikeda Sadakazu in an Azabu shrine, Tokyo.
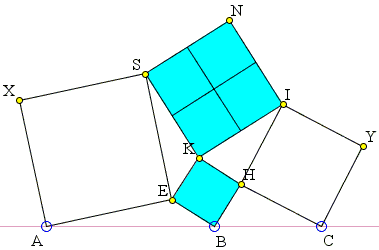
Four squares are hinged as shown. When points A, B, C are collinear, what is the relationship between the sides of squares BEKH and KINS?
Several solutions are available at this site: one makes use of Bottema's theorem, another comes from a wonderful book by Rothman and Fukagawa.
Below is a solution by Michel Cabart that employs complex numbers.
Let a, c, e, h, k, j be the complex numbers corresponding to points A, C, E, H, K, I, with the origin being in point B. Then:
j - k = (j - h) + (h - k) = i(c - h) - ih = -i(2h - c)
s - k = (s - e) + (e - k) = -i(a - ih) - h = -ai - 2h
j - k = -i(s - k) so that h = (c - ai)/4.
Replacing value of h in j - k, we get j - k = (i/2)(c + ai) = 2ih', (where h' denotes the conjugate of h) so that
This solution yields an additional result: the axis of symmetry of lines (IK) and (BH) is inclined by 45° on line (BC).
(Note: the problem we just discussed serves an example of application of complex numbers in geometry. There are many more.)
References
- H. Fukagawa, A. Rothman, Sacred Geometry: Japanese Temple Geometry, Princeton University Press, 2008, p. 149
Bottema's Theorem
- Bottema's Theorem
- An Elementary Proof of Bottema's Theorem
- Bottema's Theorem - Proof Without Words
- On Bottema's Shoulders
- On Bottema's Shoulders II
- On Bottema's Shoulders with a Ladder
- Friendly Kiepert's Perspectors
- Bottema Shatters Japan's Seclusion
- Rotations in Disguise
- Four Hinged Squares
- Four Hinged Squares, Solution with Complex Numbers
- Pythagoras' from Bottema's
- A Degenerate Case of Bottema's Configuration
- Properties of Flank Triangles
- Analytic Proof of Bottema's Theorem
- Yet Another Generalization of Bottema's Theorem
- Bottema with a Product of Rotations
- Bottema with Similar Triangles
- Bottema in Three Rotations
- Bottema's Point Sibling
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73561205
