Bottema's Theorem: What Is It?
A Mathematical Droodle

16 April 2015, Created with GeoGebra

Bottema's Theorem

Bottema's theorem

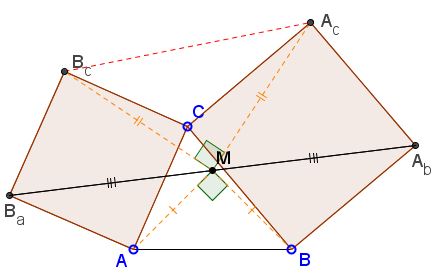
Consider a configuration of two squares ACB_cB_a and BCA_cA_b with a common vertex C. Bottema's theorem claims that the midpoint M of the segment A_bB_a is independent of C.

The reason for the naming convention is that the configuration appears as a part of a more symmetric - with respect to the letters A, B, C - configuration of three squares constructed on the sides of a triangle, see Bride's Chair. The theorem relates to Neuberg's theorem, a problem by Thébault and the Fundamental Theorem of Directly Similar Figures.

The theorem is easily proved with complex numbers.

Assume the vertices A, B, and C are represented by the complex numbers α, β, and γ, respectively. Multiplication by the imaginary number i is equivalent to rotation through p/2 in the counterclockwise direction. Mulitplication by 1/i = -i does a similar job but in the clockwise direction. We then have:

	B_a = α + (γ - α)·i,
	A_b = β + (γ - β)·(-i),

so that

(A_b + B_a)/2 = (α + β)/2 + (β - α)·i/2

independent of C = γ. The latter identity also shows that ΔAMB is right-angled and isosceles.

Here's an additional touch. Point M plays exactly the same role for triangle ΔABC as it does for ΔA_cB_cC. (Just turn the diagram upside down!) Therefore, ΔA_cMB_c is also right-angled and isosceles.

(Professor W. McWorter observed an additional property of Bottema's configuration and also that the squares can be replaced with arbitrary similar parallelograms.)

Bottema's theorem entered mathematical folklore in an adventurous guise. To make the connection clear, I shall add in parentheses points referring to the applet's diagram.

Someone found in his attic an old Description of a pirate who died long time ago. It read as follows: Go to the island X, start at the gallows (C), go to the elm tree (B) and count the steps. Then turn left by 90°, go the same number of steps and mark the point (A_b). Again, go to the gallows (C) and go from there to the fig tree (A) counting steps. Turn 90° right and proceed the same number of steps. Mark the point (B_a). A treasure is buried midway between the two marked points. The fellow travelled to the island and found the fig and the elm trees, but could not locate the gallows. Still, he was able to find and dig out the treasure. How did he do that?

Bottema's theorem helps solve a Japanese Sangaku.

Also, Bottema's theorem can be seen as a particular case of the fundamental fact that a product of two rotations is a rotation through an angle equal to the sum of two rotation angles. For example, C is the image of B_a under the rotation through 90° around A and A_b is the image of C under the rotation through 90° around B. Thus the product of the two rotations is a rotation through 180° (central symmetry), with the center of rotation located at the center of the square formed on AB. This view on Bottema's problem helps easily solve an analogue wherein equilateral triangles are constructed on the side AC, BC instead of the squares.

(Note: the problem we just discussed serves an example of application of complex numbers in geometry. There are many more.)

References

A. Engel, Problem-Solving Strategies, Springer Verlag, 1998, p. 295