Malfatti's Problem

Malfatti's problem serves a miniature example of broader, often torturous, mathematical evolution. It has started with an apparently practical problem: to cut out of a triangular prism of a material such as marble, three circular columns of the greatest possible volume. The problem (now dubbed the marble problem [Martin, p.92]) has been published in 1803 by G. Malfatti. The problem is naturally reduced to a planar problem of packing into a given triangle three circles of the largest total area. In his solution, Malfatti assumed that the three circles in the marble problem must touch each other and each touch two sides of the triangle. Thus he reduced the problem to the one that now bears his name, Malfatti's problem [Dörrie, 147]:

To draw within a given triangle three circles each of which is tangent to the other two and to two sides of the triangle.

It is said that a century earlier Jacob Bernoulli considered the problem for an isosceles triangle, which, if true, would have enhanced its standing in the mathematical community. (The problem also occurs in Japanese temple geometry where it is often attributed to Chokuyen Naonobu Ajima, 1732-1798.) The problem received a serious boost in 1826 when J. Steiner published (without a proof!) an elegant solution, probably with a purpose of demonstrating the power of his methods. Following is a short history of further development [Bottema]:

Steiner has also considered extensions of the problem and given solutions. The first is the one where the sides lines of the triangle are replaced by circles. Further generalizations concern the figures of three circles on a sphere, and of three conic sections on a quadric surface. In the nineteenth century many mathematicians have worked on this problem. Among these were Cayley (1852), Schellbach (who in 1853 published a very nice goniometric solution), and Clebsch (who in 1857 extended Schellbach’s solution to three conic sections on a quadric surface, and for that he made use of elliptic functions). If one allows in Malfatti’s original problem also escribed and internally tangent circles, then there are a total of 32 (real) solutions. One can find all these solutions mentioned by Pampuch (1904). The generalizations mentioned above even have, as appears from investigation by Clebsch, 64 solutions.

In 1929 Lob and Richmond showed by counterexample that in the case of an equilateral triangle the Malfatti circles (the triad of circles that solves Malfatti's problem) are not optimal in the sense that they do not answer the marble problem. Lob and Richmond showed that a different circle configuration that consists of the incircle and two circles packed in the corners of the triangle beats Malfatti's construction. In 1967, M. Goldberg gave a graphical evidence that, as a matter of fact, the Malfatti circles never solve the original marble problem. In 1992 (appeared in English in 1994), Zalgaller and Los gave a complete solution to the latter.

When the three circles in Steiner's generalization are pairwise tangent externally, the problem is trivialized by inversion [Bottema]. An inversion with center in one of the points of tangency, inverts two circles into two parallel lines:

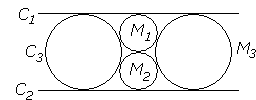
where C₁, C₂, C₃ are the inversions of the given circles, while M₁, M₂, M₃ invert back into Malfatti's circles for the generalized problem.

Of the texts available to me and listed below, Dörrie gives a mostly analytic but otherwise an elementary solution by Schellbach. Martin seems to follow a similar solution by Malfatti himself. Coolidge, F. G.-M., Hadamard, Shklyarsky all follow in Steiner's footsteps, but with different proofs. The latter does not mention either Malfatti or Steiner. Wells describes the problem without proof, gives a short historic outline and provides counterexamples.

The applet below illustrates Steiner's solution for ΔABC:

Draw three angle bisectors IA, IB, IC.
In the triangles IAB, IBC, ICA inscribe circles C_c, C_a, C_b. Note that the angle bisectors serve as common internal tangents for pairs of these circles.
For each pair of the circles consider the second internal tangents. The latter concur in a point (L) and cross the sides in points M, P, T, as shown in the applet.
The three quadrilaterals APLT, BMLP, and CTLM are inscriptible. Their incircles solve Malfatti's problem.

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at https://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

What if applet does not run?

The proof appears elsewhere.

References

O. Bottema, The Malfatti Problem, Forum Geometricorum, v 1 (2000), pp. 43-50 (Ttranslation by F. van Lamoen of an 1949 article)
J. L. Coolidge, A Treatise On the Circle and the Sphere, AMS - Chelsea Publishing, 1971
H. Dörrie, 100 Great Problems Of Elementary Mathematics, Dover Publications, NY, 1965.
F. G.-M., Exercices de Géométrie, Éditions Jacques Gabay, sixiéme édition, 1991, pp. 726-728
H. Fukagawa, D. Pedoe, Japanese Temple Geometry Problems, The Charles Babbage Research Center, Winnipeg, 1989
M. Goldberg, On the Original Malfatti Problem, Math. Mag. 40, 241-247, 1967.
J. Hadamard, Leçons de géométrie élémentaire, tome I, 13e édition, reprint 1988
G. E. Martin, A Geometric Constructions, Springer, 1998
D. O. Shklyarsky, N. N. Chentsov, I. M. Yaglom, Selected Problems and Theorems of Elementary Mathematics, v 2, Moscow, 1952 (in Russian)
D. Wells, The Penguin Book of Curious and Interesting Puzzles, Penguin Books, 1992

Sangaku

71945882