Inscriptible and Exscriptible Quadrilaterals

Two tangents from a point outside a circle to the circle are equal. This simple result leads to a criterion for a quadrilateral to be inscriptible. A convex quadrilateral is inscriptible if there exists a circle touching all four of its sides. (A more colorful, but less verbose illustration is available elsewhere.) If the lengths of the tangents from vertices A, B, C, D of a quadrilateral circumscribed around a circle are denoted a, b, c, d, then

(1)	AB = a + b, BC = b + c, CD = c + d, DA = d + a,

from which

(2)

AB + CD = BC + DA.

In a quadrilateral circumscribed around a circle the sum of two opposite sides equals to the sum of two remaining (and opposite) sides. The French geometer F. G.-M. attributes [Exercices, p. 316, note no 744) this statement to a French engineer Pitot (1725). The converse that appears to have been only proved in the 19^th is also true: (2) implies existence of a circle that touches all four sides of the quadrilateral ABCD. In a certain disguise the converse has been shown by J.-R. Durande (1815), but later approached directly by J. Steiner (1846).

Assume ABCD is a convex quadrilateral such that (2) holds. It is possible to find a circle tangent to three side lines, AB, BC, and CD, for example by considering the bisectors of angles B and C. The idea is to show that the remaining side DA is also tangent to that circle.

Assume it is not. Draw a tangent from A (different from AB) and let it intersect CD in D₀. By Pitot's theorem,

(2')

AB + CD₀ = BC + D₀A.

From (2) and (2')

CD - CD₀ = DA - D₀A.

But C, D and D₀ are collinear, so that CD - CD₀ = DD₀ (or the other way round if we wish to avoid working with negative length.) This means that in an apparently non-degenerate triangle CDD₀, one of the sides equals the difference of the other two:

DD₀ = DA - D₀A.

This would contradict the triangle inequality, which proves the converse.

Note

The above proof has a flaw that is analyzed elsewhere.

Both Pitot's theorem and its converse have an analogue in the case where a circle tangent to the four sidelines of quadrilateral ABCD lies in the exterior of the quadrilateral. It is natural to brand a quadrilateral for which such a circle exists exscriptible, although I am not sure that this is a common practice.

There are two ways in which a simple quadrilateral can be exscriptible:

Figure 1

It is easy to see that in both cases there exists a pair of adjacent sides the sum of whose length equals the sum of the remaining two sides. In both cases we have

(3)

AB + BC = CD + DA.

Note that the same is true for a self-intersecting quadrilateral as well.

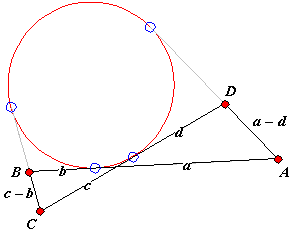
The converse is also true, and its proof is basically the same as in the inscriptible case. F. G.-M. (p. 319, note 748) ascribes the theorem and its converse to J. Steiner (1846). The fact that (3) is necessary and sufficent for the exscriptible case has an interesting repercussion. Let's overlay the two cases in Figure 1 into a single quadrangle.

Obviously quadrilaterals ABCD and AB'CD' are either both exscriptible or both are not exscriptible. In other words, if one of them is exscriptible, so is the other. For ABCD the condition is (3). For AB'CD' (3) should be rewritten as

(3')

AB' + B'C = CD' + D'A.

It follows that (3) implies (3') and vice versa. This fact is known as Urquhart's theorem, after an Australian mathematician L. M. Urquhart. Urquhart named it "The most elementary theorem of Euclidean geometry" for the simple reason that it talks only of straight lines and their lengths. (You may want to check a short trigonometric proof of the theorem.)

References

F. G.-M., Exercices de Géométrie, Éditions Jacques Gabay, sixiéme édition, 1991, pp. 1175-1177

Urquhart's Theorem

71545679