Incenters in Cyclic Quadrilateral:
What is this about?
A Mathematical Droodle

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

Incenters in Cyclic Quadrilateral

Every (convex) quadrilateral ABCD defines four triangles: BCD, ACD, ABD, and ABC. The applet is an attempt to convey an assertion often referred to as the Japanese theorem:

The incenters of the four triangles form a rectangle.

Japanese theorem: rectangle in a cyclic quadrilateral

Proof

From ΔBCD, ∠BIBCDC = 90° + ∠BDC/2.

Similarly, from ΔABC, ∠BIABCC = 90° + ∠BAC/2.

However, since we assumed that the quadrilateral ABCD is cyclic, ∠BDC = ∠BAC. Therefore, also ∠BIBCDC = ∠BIABCC. The quadrilateral BIABCIBCDC is therefore cyclic, so that

(1) ∠BCIBCD + ∠BIABCIBCD = 180°.

Similarly the quadrilateral AIABDIABCB is cyclic, so that

(2) ∠BAIABD + ∠BIABCIABD = 180°.

(1) and (2) imply that

∠BIABCIBCD + ∠BIABCIABD = 360° - ∠BCD/2 - ∠BAD/2 = 270°.

Which gives

(3) ∠IABDIABCIBCD = 90°.

Other angles are treated similarly. Q.E.D.

In addition, let P, Q, R, and S be the midpoints of the arcs AB, CD, BC, and AD, respectively.

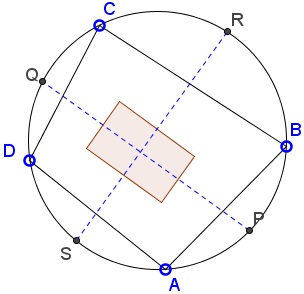
arc bisectors in a cyclic quadrilateral

It's almost immediate to prove that PQ⊥RS. This is also true that PQ and RS are parallel to the sides of the rectangle of the incenters and pass through their midpoints.

This is #3.5 from Fukagawa and Pedoe's collection. It was written on a 1880 tablet in the Yamagata prefecture. Maruyama Ryoukan posted a tablet in 1800 at the Sannosha shrine in Tsuruoka city of Yamagata prefecture with the observation that [Fukagawa and Rothman, p. 192]

rABC + rACD = rABD + rBCD.

(In itself, this is a particular case of what is known as the Old Japanese Theorem.)

This implies that the lines through the incenters parallel to the diagonals form a rhombus.

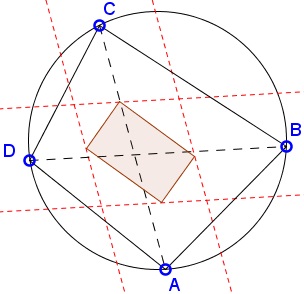
rhombus in a cyclic quadrilateral

You may observe that the arc bisectors of the arcs subtended by the sides of the quadrilateral serve as the diagonals of the rhombus.

References

  1. H. Fukagawa, D. Pedoe, Japanese Temple Geometry Problems, The Charles Babbage Research Center, Winnipeg, 1989

    Write to:

    Charles Babbage Research Center
    P.O. Box 272, St. Norbert Postal Station
    Winnipeg, MB
    Canada R3V 1L6

  2. H. Fukagawa, A. Rothman, Sacred Geometry: Japanese Temple Geometry, Princeton University Press, 2008
  3. D. Wells, You Are A Mathematician, John Wiley & Sons, 1995

Sangaku

  1. Sangaku: Reflections on the Phenomenon
  2. Critique of My View and a Response
  3. 1 + 27 = 12 + 16 Sangaku
  4. 3-4-5 Triangle by a Kid
  5. 7 = 2 + 5 Sangaku
  6. A 49th Degree Challenge
  7. A Geometric Mean Sangaku
  8. A Hard but Important Sangaku
  9. A Restored Sangaku Problem
  10. A Sangaku: Two Unrelated Circles
  11. A Sangaku by a Teen
  12. A Sangaku Follow-Up on an Archimedes' Lemma
  13. A Sangaku with an Egyptian Attachment
  14. A Sangaku with Many Circles and Some
  15. A Sushi Morsel
  16. An Old Japanese Theorem
  17. Archimedes Twins in the Edo Period
  18. Arithmetic Mean Sangaku
  19. Bottema Shatters Japan's Seclusion
  20. Chain of Circles on a Chord
  21. Circles and Semicircles in Rectangle
  22. Circles in a Circular Segment
  23. Circles Lined on the Legs of a Right Triangle
  24. Equal Incircles Theorem
  25. Equilateral Triangle, Straight Line and Tangent Circles
  26. Equilateral Triangles and Incircles in a Square
  27. Five Incircles in a Square
  28. Four Hinged Squares
  29. Four Incircles in Equilateral Triangle
  30. Gion Shrine Problem
  31. Harmonic Mean Sangaku
  32. Heron's Problem
  33. In the Wasan Spirit
  34. Incenters in Cyclic Quadrilateral
  35. Japanese Art and Mathematics
  36. Malfatti's Problem
  37. Maximal Properties of the Pythagorean Relation
  38. Neuberg Sangaku
  39. Out of Pentagon Sangaku
  40. Peacock Tail Sangaku
  41. Pentagon Proportions Sangaku
  42. Proportions in Square
  43. Pythagoras and Vecten Break Japan's Isolation
  44. Radius of a Circle by Paper Folding
  45. Review of Sacred Mathematics
  46. Sangaku à la V. Thebault
  47. Sangaku and The Egyptian Triangle
  48. Sangaku in a Square
  49. Sangaku Iterations, Is it Wasan?
  50. Sangaku with 8 Circles
  51. Sangaku with Angle between a Tangent and a Chord
  52. Sangaku with Quadratic Optimization
  53. Sangaku with Three Mixtilinear Circles
  54. Sangaku with Versines
  55. Sangakus with a Mixtilinear Circle
  56. Sequences of Touching Circles
  57. Square and Circle in a Gothic Cupola
  58. Steiner's Sangaku
  59. Tangent Circles and an Isosceles Triangle
  60. The Squinting Eyes Theorem
  61. Three Incircles In a Right Triangle
  62. Three Squares and Two Ellipses
  63. Three Tangent Circles Sangaku
  64. Triangles, Squares and Areas from Temple Geometry
  65. Two Arbelos, Two Chains
  66. Two Circles in an Angle
  67. Two Sangaku with Equal Incircles
  68. Another Sangaku in Square
  69. Sangaku via Peru
  70. FJG Capitan's Sangaku

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

70767614