R. Honsberger,
Mathematical Gems, III,
MAA, 1985, pp. 24-26

In Roger Johnson's marvellous old geometry text-Advanced Euclidean Geometry, first published in 1929 - he reports (on page 193 of the Dover edition, 1960) on the ancient custom by Japanese mathematicians of inscribing their discoveries on tablets which were hung in the temples to the glory of the gods and the honor of the authors. The following gem is known to have been exhibited in this way in the year 1800.

A great deal more might have been claimed, for this same sum results for every way of triangulating the polygon! (Figure 2). As we shall see, a simple application of a beautiful theorem of L. N. M. Carnot (1753-1823) settles the whole affair.

First of all, observe that any triangulation of an n-gon with its diagonals consists of (n-2) triangles. Next assume that the triangles in the triangulation are numbered, and that the inradius of triangle i is r_i; moreover, denote the sum of distances in the Carnot’s theorem as OO_i. Then, observing that every triangle in the triangulation has the given circle as its circumcircle, Carnot’s thereom states

and the sum in question is given by

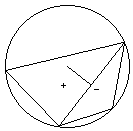
Note now that the sum OO₁ + OO₂ + … + OO_n-2 on the right consists of perpendiculars to the sides of the polygon each counted once, and perpendiculars to the diagonals each counted twice since every diagonal serves as a side of two adjacent triangles. Furthermore, considering such internal perpendiculars, each is taken once with the sign plus and another time with the sign minus thus contributing nothing to the sum. Therefore, this sum is actually equal to the sum of all perpendiculars from O to the sides of the polygon. And, therefore, the right-hand side in (*) is constant. So is the left-hand side.

(There is another theorem that is also known as Japanese.)

References

1. R. Honsberger, Mathematical Gems III, MAA, 1985

Sangaku

1. Sangaku: Reflections on the Phenomenon
2. Critique of My View and a Response
3. 1 + 27 = 12 + 16 Sangaku
4. 3-4-5 Triangle by a Kid
5. 7 = 2 + 5 Sangaku
6. A 49^th Degree Challenge
7. A Geometric Mean Sangaku
8. A Hard but Important Sangaku
9. A Restored Sangaku Problem
   • A better solution to a difficult sangaku problem
10. A Sangaku: Two Unrelated Circles
11. A Sangaku by a Teen
12. A Sangaku Follow-Up on an Archimedes' Lemma
13. A Sangaku with an Egyptian Attachment
14. A Sangaku with Many Circles and Some
15. A Sushi Morsel
16. An Old Japanese Theorem
17. Archimedes Twins in the Edo Period
18. Arithmetic Mean Sangaku
19. Bottema Shatters Japan's Seclusion
20. Circles and Semicircles in Rectangle
21. Circles in a Circular Segment
22. Circles Lined on the Legs of a Right Triangle
23. Equal Incircles Theorem
24. Equilateral Triangle, Straight Line and Tangent Circles
25. Equilateral Triangles and Incircles in a Square
26. Five Incircles in a Square
27. Four Hinged Squares
28. Four Incircles in Equilateral Triangle
29. Gion Shrine Problem
30. Harmonic Mean Sangaku
31. Heron's Problem
32. In the Wasan Spirit
33. Incenters in Cyclic Quadrilateral
34. Japanese Art and Mathematics
35. Malfatti's Problem
36. Maximal Properties of the Pythagorean Relation
37. Neuberg Sangaku
38. Out of Pentagon Sangaku
39. Peacock Tail Sangaku
40. Pentagon Proportions Sangaku
41. Pythagoras and Vecten Break Japan's Isolation
42. Radius of a Circle by Paper Folding
43. Review of Sacred Mathematics
44. Sangaku à la V. Thebault
45. Sangaku and The Egyptian Triangle
46. Sangaku in a Square
47. Sangaku Iterations, Is it Wasan?
48. Sangaku with 8 Circles
49. Sangaku with Three Mixtilinear Circles
50. Sangaku with Versines
51. Sangakus with a Mixtilinear Circle
52. Sequences of Touching Circles
53. Square and Circle in a Gothic Cupola
54. Tangent Circles and an Isosceles Triangle
55. The Squinting Eyes Theorem
56. Steiner's Sangaku
57. Three Incircles In a Right Triangle
58. Three Squares and Two Ellipses
59. Three Tangent Circles Sangaku
60. Triangles, Squares and Areas from Temple Geometry
61. Two Arbelos, Two Chains
62. Two Circles in an Angle
63. Two Sangaku with Equal Incircles

Copyright © 1996-2009 Alexander Bogomolny