Conic in Mixtilinear Incircles
What Might This Be About?
Problem
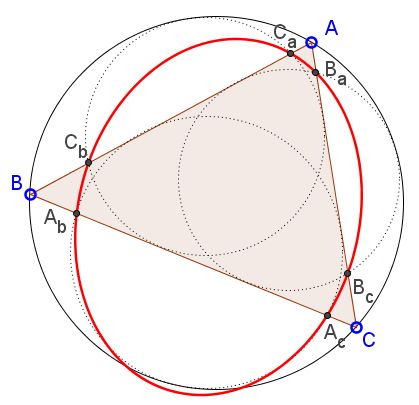
The six points of intersection of the mixtilinear incircles with the sides of a triangle lie on a conic.
Solution
Let the points of intersection be $A_b,$ $A_c,$ etc. as shown in the diagram.$

According to Carnot's Theorem for Conics, the six points will lie on a conic, provided
\(\displaystyle \big(\frac{AC_a}{BC_a}\cdot\frac{AC_b}{BC_b}\big)\cdot\big(\frac{BA_b}{CA_b}\cdot\frac{BA_c}{CA_c}\big)\cdot\big(\frac{CB_c}{AB_c}\cdot\frac{CB_a}{AB_a}\big)=1. \)
Let $K$ and $M$ be the points of tangency of two of the mixtilinear incircles with side $AC.$

Then, by the Power of a Point Theorem,
$AC_a\cdot AC_b=AK^{2}$ and $CA_b\cdot CA_c=CM^{2}.$
Now, we know that $AK=\displaystyle\frac{ab}{p}$ and $CM=\displaystyle\frac{bc}{p},$ where $a,b,c$ are the side lengths opposite vertices $A,B,C$ and $p=(a+b+c)/2$ the semiperimeter. The other elements in Carnot's criterion are defined cyclically, and this is why the condition holds: upon substitution all the terms cancel out.
\(\displaystyle \bigg(\frac{ab/p}{ab/p}\cdot\frac{bc/p}{bc/p}\cdot\frac{ac/p}{ac/p}\bigg)^{2}=1. \)
Acknowledgment
The problem has been conjectured by Emmanuel Antonio José García; the solution at the community blog of the artofproblemsolving site is due to Ivan Zelich.
![]()
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73601657
