Construction and Properties of Mixtilinear Incircles
What Might This Be About?
Introduction
Mixtilinear incircle is a circle tangent to two sides of a triangle and to the triangle's circumcircle. In every triangle there are three mixtilinear incircles, one for each vertex. The diagram below shows the mixtilinear incircle corresponding to vertex $B$ in $\Delta ABC:$
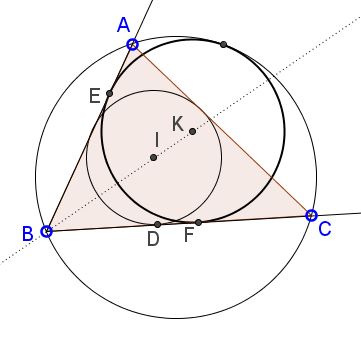
Problem
Let $C(K)$ be the mixtilinear incircle in $\Delta ABC$ touching side $AB$ at $E,$ side $BC$ at $F.$ Let, as usual, $a,$ $b,$ $c$ be the sides lengths opposite vertices $A,$ $B,$ and $C,$ respectively; $p=(a+b+c)/2$ the semiperimeter; $I$ the incenter of $\Delta ABC.$

Then
$\displaystyle BE=BF=\frac{ac}{p}.$
$EF\perp BI$ and $I\in EF.$
Solution
Consider an inversion in the circle $C(B,\sqrt{ac}).$
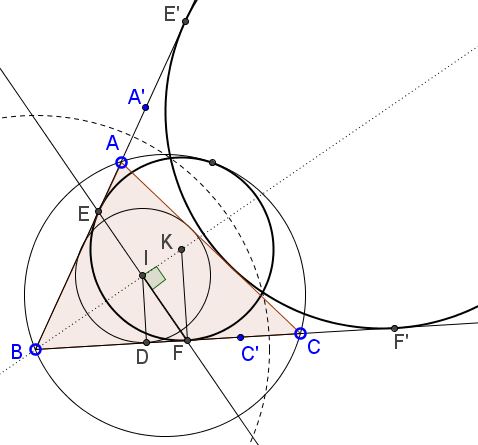
Let a generic point $X$ be mapped on point $X'.$ Since $BA\cdot BA'=ac,$ $BA'=c;$ similarly, $BC'=a.$ It follows that $\Delta ABC=\Delta A'BC'.$ The circumcircle $(ABC)$ maps onto a straight line passing through both $A'$ and $C'$ such that it maps onto $A'C'.$ Thus the image of the mixtilinear circle is tangent to the three lines $BA$ (i.e., $BA'$), $BC$ (i.e., $BC'$), and $A'C',$ and, is, therefore, the excircle of $\Delta A'BC'.$ Because of the symmetry in the angle bisector $BI,$ it is also tangent to $AC$ and so is the excircle of $\Delta ABC.$
Now, it is easy to see that $BF'=p,$ making $BF=\displaystyle\frac{ac}{p}$ and, thus proving the first part.
For the second part, recollect that $BI^{2}=\displaystyle\frac{(p-b)ac}{p},$ whereas $BD=p-b,$ where $D$ is the point of tangency of the incircle $(I)$ with side $BC.$ We then have
$\displaystyle\frac{BI^2}{BF^2}=\frac{(p-b)ac}{p}\cdot\frac{p^2}{(ac)^2}=\frac{p(p-b)}{ac}.$
On the other hand,
$\displaystyle\frac{BD^2}{BI^2}=\frac{(p-b)^{2}p}{(p-b)ac}=\frac{p(p-b)}{ac}.$
This shows that $BI^{2}=BD\cdot BF,$ making $\Delta BIF$ right (at $I.)$
Note that this property explains the construction of mixtilinear circles discussed elsewhere.
Acknowledgment
I was pointed to the proof of the first relation at the community blog of the artofproblemsolving site by Emmanuel Antonio José García.
Inversion - Introduction
- Angle Preservation Property
- Apollonian Circles Theorem
- Archimedes' Twin Circles and a Brother
- Bisectal Circle
- Chain of Inscribed Circles
- Circle Inscribed in a Circular Segment
- Circle Inversion: Reflection in a Circle
- Circle Inversion Tool
- Feuerbach's Theorem: a Proof
- Four Touching Circles
- Hart's Inversor
- Inversion in the Incircle
- Inversion with a Negative Power
- Miquel's Theorem for Circles
- Peaucellier Linkage
- Polar Circle
- Poles and Polars
- Ptolemy by Inversion
- Radical Axis of Circles Inscribed in a Circular Segment
- Steiner's porism
- Stereographic Projection and Inversion
- Tangent Circles and an Isosceles Triangle
- Tangent Circles and an Isosceles Triangle II
- Three Tangents, Three Secants
- Viviani by Inversion
- Simultaneous Diameters in Concurrent Circles
- An Euclidean Construction with Inversion
- Construction and Properties of Mixtilinear Incircles
- Two Quadruplets of Concyclic Points
- Seven and the Eighth Circle Theorem
- Invert Two Circles Into Equal Ones
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73595818
