Four Incircles in an Equilateral Triangle, Third Solution
Elsewhere we described and solved the following sangaku:
In an equilateral triangle \(ABC\) the lines \(BEF\), \(CFD\), \(ADE\) are drawn making equal angles with \(AB\), \(BC\), \(CA\), respectively, forming the triangle \(DEF\), and so that the radius of the incircle of triangle \(DEF\) is equal to the radii of the incircles of triangles $ABE,$ $BCF,$ and $ACD.$
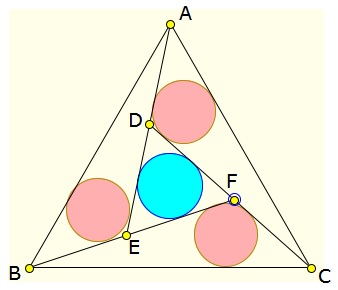
Find \(DE\) in terms of \(AB\).
The solution below is by J. John Samuel (7 MAy, 2014). Like George Zettler, John first establishes the basic facts, viz.,
- The area $A$ of a triangle with the semiperimeter $p$ and the inradius $r$ equals $A=pr.$
- In an equilateral triangle the side length $a$ and the inradius $r$ are related through $a = 2\sqrt{3}r.$
- With the reference to the above diagram, in $\Delta ABE,$ the altitude $h$ from vertex $B$ equals $\displaystyle h=\frac{\sqrt{3}}{2}BE.$
Next, with a change of notations reflected in the diagram below,
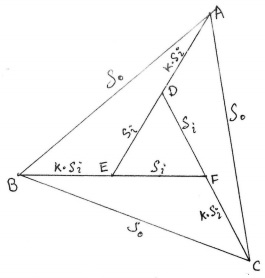
John derives the expression
$\displaystyle \frac{S_{o}^{2}}{S_{i}^{2}}=3k(k+1)+1,$
where $S_{o}$ and $S_{i}$ are the side lengths of the $o$uter and the $i$nner equilateral triangles. The easiest way to see that is to observe that, say, in $\Delta ABE,$ the Law of Cosines gives
$S_{o}^{2}=((kS_{i})^{2}+(kS_{i})((k+1)S_{i})+((k+1)S_{i})^{2}=(S_{i})^{2}(k^{2}+k(k+1)+(k+1)^{2}).$
The final step is illustrated by a diagram and a moving observation:

We may find the relationship between $S_{o}$ and $S_{i}$ in yet another way, through the area formula $A=pr:$
$\displaystyle\begin{align} Area(\Delta ABE) &= \frac{1}{2}(S_{o}+kS_{i}+(k+1)S_{i})R\\ &=\frac{1}{2}\frac{S_{i}}{2\sqrt{3}}(S_{o}+(2k+1)S_{i})\\ &=\frac{S_{i}}{4\sqrt{3}}(S_{o}+(2k+1)S_{i}). \end{align}$
On the other hand,
$\displaystyle\begin{align} Area(\Delta ABE) &= \frac{1}{2}h\cdot AE\\ &=\frac{1}{2}\frac{\sqrt{3}}{2}(kS_{i})((k+1)S_{i})\\ &=\frac{\sqrt{3}}{4}S_{i}^{2}k(k+1). \end{align}$
Comparing the two expressions, we obtain $S_{o}=S_{i}(3k^{2}+k-1),$ which leads to an equation for k:
$\displaystyle\frac{S_{o}^{2}}{S_{i}^{2}}=(3k^{2}+k-1)^{2}=3k(k+1)+1.$
This is a fourth degree equation. Undeterred, we proceed to simplify:
$\displaystyle\begin{align} 3k(k+1)+1 &= (3k^{2}+k-1)^{2}\\ &=9k^{4}+6k^{3}-5k^{2}-2k+1, \end{align}$
or, $9k^{4}+6k^{3}-8k^{2}-5k=0.$ $k=0,$ not fitting the context of the problem can be cancelled out: $9k^{3}+6k^{2}-8k-5=0.$ In addition, we may notice (and John does) that $-9+6+8-5=0,$ implying that $k=-1$ is another irrelevant root of the equation. Dividing by $k+1$ leaves $9k^{2}-3k-5=0,$ with the roots $\displaystyle\frac{3\pm\sqrt{189}}{18}=\frac{1\pm\sqrt{21}}{6}.$ Dropping the negative root, we are left with the only suitable solution
$\displaystyle k=\frac{1+\sqrt{21}}{6}. $
Now we are in a position to solve the problem:
$\displaystyle \frac{S_{o}}{S_{i}}=3k^{2}+k-1=\frac{3+\sqrt{21}}{3}. $
From this
$\displaystyle \frac{S_{i}}{S_{o}}=\frac{3}{3+\sqrt{21}}=\frac{3(\sqrt{21}-3)}{21-9}=\frac{\sqrt{21}-3}{4}. $
This agrees with the solutions of George Zettler and Angela Drei.
- Sangaku: Reflections on the Phenomenon
- Critique of My View and a Response
- 1 + 27 = 12 + 16 Sangaku
- 3-4-5 Triangle by a Kid
- 7 = 2 + 5 Sangaku
- A 49th Degree Challenge
- A Geometric Mean Sangaku
- A Hard but Important Sangaku
- A Restored Sangaku Problem
- A Sangaku: Two Unrelated Circles
- A Sangaku by a Teen
- A Sangaku Follow-Up on an Archimedes' Lemma
- A Sangaku with an Egyptian Attachment
- A Sangaku with Many Circles and Some
- A Sushi Morsel
- An Old Japanese Theorem
- Archimedes Twins in the Edo Period
- Arithmetic Mean Sangaku
- Bottema Shatters Japan's Seclusion
- Chain of Circles on a Chord
- Circles and Semicircles in Rectangle
- Circles in a Circular Segment
- Circles Lined on the Legs of a Right Triangle
- Equal Incircles Theorem
- Equilateral Triangle, Straight Line and Tangent Circles
- Equilateral Triangles and Incircles in a Square
- Five Incircles in a Square
- Four Hinged Squares
- Four Incircles in Equilateral Triangle
- Four Incircles in an Equilateral Triangle, a Sangaku
- Gion Shrine Problem
- Harmonic Mean Sangaku
- Heron's Problem
- In the Wasan Spirit
- Incenters in Cyclic Quadrilateral
- Japanese Art and Mathematics
- Malfatti's Problem
- Maximal Properties of the Pythagorean Relation
- Neuberg Sangaku
- Out of Pentagon Sangaku
- Peacock Tail Sangaku
- Pentagon Proportions Sangaku
- Proportions in Square
- Pythagoras and Vecten Break Japan's Isolation
- Radius of a Circle by Paper Folding
- Review of Sacred Mathematics
- Sangaku à la V. Thebault
- Sangaku and The Egyptian Triangle
- Sangaku in a Square
- Sangaku Iterations, Is it Wasan?
- Sangaku with 8 Circles
- Sangaku with Angle between a Tangent and a Chord
- Sangaku with Quadratic Optimization
- Sangaku with Three Mixtilinear Circles
- Sangaku with Versines
- Sangakus with a Mixtilinear Circle
- Sequences of Touching Circles
- Square and Circle in a Gothic Cupola
- Steiner's Sangaku
- Tangent Circles and an Isosceles Triangle
- The Squinting Eyes Theorem
- Three Incircles In a Right Triangle
- Three Squares and Two Ellipses
- Three Tangent Circles Sangaku
- Triangles, Squares and Areas from Temple Geometry
- Two Arbelos, Two Chains
- Two Circles in an Angle
- Two Sangaku with Equal Incircles
- Another Sangaku in Square
- Sangaku via Peru
- FJG Capitan's Sangaku
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73518793
