Equal Incircles Theorem, Angela Drei's Proof

The Equal Incircle Theorem is a generalization of a sangaku problem:

Let C be a point. Assume points Mi, I = 1, 2, ..., N (N > 3) lie on a line not through C. Assume further that the incircles of triangles M1CM2, M2CM3, ..., MN-1CMN all have equal radii. Then the same is true of triangles M1CM3, M2CM4, ..., MN-2CMN, and also of triangles M1CM4, M2CM5, ..., MN-3CMN, and so on.

The proof below is by Angela Drei, an Italian mathematics teacher. The proof first appeared in an Italian magazine Archimede. It depends on two lemmas.

Lemma 1

In any ΔABC,

1 - 2r/h = tan(α/2)tan(β/2),

where r is the inradius, h the altitude to AB, α = ∠BAC, β = ∠ABC.

Proof

Let a, b, c be the lengths sides BC, AC, AB and p = (a + b + c)/2 the semiperimeter of ΔABC. As we know,

tan²(α/2) = (p - b)(p - c) / p(p - a) and tan²(β/2) = (p - a)(p - c) / p(p - b)

Taking the product gives

tan²(α/2)tan²(β/2) = (p - c)² / p².

Next, letting S be the area of ΔABC,

 (p - c) / p= 1 - c/p
  = 1 - ch·r / pr·h
  = 1 - 2Sr / Sh
  = 1 - 2r / h,

which proves the lemma.

Lemma 2

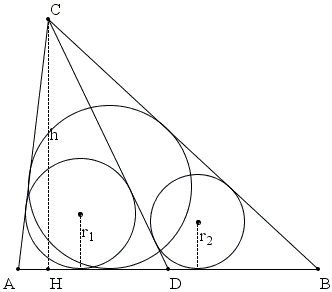
Equal incircles in two adjacent triangles

Given a triangle ABC, D lie on AB, r1 and r2 are the radii of the circles inscribed in ACD and BCD, r is the inradius, h is the length of the altitude to the side AB. Then the following relation holds:

(1 - 2r1/h)(1 - 2r2/h) = 1 - 2r/h.

In particular, if r1 = r2, then (1 - 2r1/h)² = 1 - 2r/h.

Proof

Apply Lemma 1 to triangles ACD, BCD, and ABC and observe that ∠ADC/2 = 90° - ∠BDC/2 so that tan(∠ADC/2)tan(∠BDC/2) = 1.

Lemma 2'

Assume points Mi, I = 1, 2, ..., N (N > 3) lie on side AB of ΔABC, A = M1, B = MN. Assume further that the incircles of triangles M1CM2, M2CM3, ..., MN-1CMN all have equal radii, say ρ. If, as before, h is the altitude from C and r is the inradius of ΔABC, then

(1 - 2ρ/h)N-1 = 1 - 2r/h.

Proof

Similar to the proof of Lemma 2, apply Lemma 1 to each of the triangles MiCMi+1 and multiply the identities. The products of the tangents due to pairs of supplementary angles at points Mj, j = 2, ..., N-1, all equal to 1, leaving only the product tan(α/2)tan(β/2) which is exactly (and still) 1 - 2r/h.

Proof of the Equal Incircle Theorem

This is a direct consequence of Lemma 2 applied to pairs of adjacent triangles Mi-1CMi and MiCMi+1.

Sangaku

  1. Sangaku: Reflections on the Phenomenon
  2. Critique of My View and a Response
  3. 1 + 27 = 12 + 16 Sangaku
  4. 3-4-5 Triangle by a Kid
  5. 7 = 2 + 5 Sangaku
  6. A 49th Degree Challenge
  7. A Geometric Mean Sangaku
  8. A Hard but Important Sangaku
  9. A Restored Sangaku Problem
  10. A Sangaku: Two Unrelated Circles
  11. A Sangaku by a Teen
  12. A Sangaku Follow-Up on an Archimedes' Lemma
  13. A Sangaku with an Egyptian Attachment
  14. A Sangaku with Many Circles and Some
  15. A Sushi Morsel
  16. An Old Japanese Theorem
  17. Archimedes Twins in the Edo Period
  18. Arithmetic Mean Sangaku
  19. Bottema Shatters Japan's Seclusion
  20. Chain of Circles on a Chord
  21. Circles and Semicircles in Rectangle
  22. Circles in a Circular Segment
  23. Circles Lined on the Legs of a Right Triangle
  24. Equal Incircles Theorem
    • Equal Incircle Theorem, Angela Drei's Proof
  25. Equilateral Triangle, Straight Line and Tangent Circles
  26. Equilateral Triangles and Incircles in a Square
  27. Five Incircles in a Square
  28. Four Hinged Squares
  29. Four Incircles in Equilateral Triangle
  30. Gion Shrine Problem
  31. Harmonic Mean Sangaku
  32. Heron's Problem
  33. In the Wasan Spirit
  34. Incenters in Cyclic Quadrilateral
  35. Japanese Art and Mathematics
  36. Malfatti's Problem
  37. Maximal Properties of the Pythagorean Relation
  38. Neuberg Sangaku
  39. Out of Pentagon Sangaku
  40. Peacock Tail Sangaku
  41. Pentagon Proportions Sangaku
  42. Proportions in Square
  43. Pythagoras and Vecten Break Japan's Isolation
  44. Radius of a Circle by Paper Folding
  45. Review of Sacred Mathematics
  46. Sangaku à la V. Thebault
  47. Sangaku and The Egyptian Triangle
  48. Sangaku in a Square
  49. Sangaku Iterations, Is it Wasan?
  50. Sangaku with 8 Circles
  51. Sangaku with Angle between a Tangent and a Chord
  52. Sangaku with Quadratic Optimization
  53. Sangaku with Three Mixtilinear Circles
  54. Sangaku with Versines
  55. Sangakus with a Mixtilinear Circle
  56. Sequences of Touching Circles
  57. Square and Circle in a Gothic Cupola
  58. Steiner's Sangaku
  59. Tangent Circles and an Isosceles Triangle
  60. The Squinting Eyes Theorem
  61. Three Incircles In a Right Triangle
  62. Three Squares and Two Ellipses
  63. Three Tangent Circles Sangaku
  64. Triangles, Squares and Areas from Temple Geometry
  65. Two Arbelos, Two Chains
  66. Two Circles in an Angle
  67. Two Sangaku with Equal Incircles
  68. Another Sangaku in Square
  69. Sangaku via Peru
  70. FJG Capitan's Sangaku

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

71868978