A 49^th Degree Challenge

I always thought of Sangaku as Temple Geometry, although many of the tablets posed problem in algebra and calculus. Here is one example from [Fukagawa and Rothman]. The tablet may still be seen at the Asahikanzeon temple in Sabae. It was presented by Momota in 1807 and recorded in his travel diary by Yamaguchi Kanzan.

The tablet asks for a solution in integers to a system of three equations

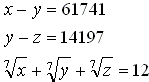
The tablet gives a solution to this particular system, viz.,

and also derives an equation of degree 49 for a more general problem. While it is not difficult to find the above triple by a simple trial-and-error method, even deriving the 49^th degree equation as has been done by Momota is a challenge.

Let me know if you find a way to perform the feat.

References

1. H. Fukagawa, A. Rothman, Sacred Mathematics: Japanese Temple Geometry, Princeton University Press, 2008, pp. 252-253

Sangaku

1. Sangaku: Reflections on the Phenomenon
2. Critique of My View and a Response
3. 1 + 27 = 12 + 16 Sangaku
4. 3-4-5 Triangle by a Kid
5. 7 = 2 + 5 Sangaku
6. A 49^th Degree Challenge
7. A Geometric Mean Sangaku
8. A Hard but Important Sangaku
9. A Sangaku: Two Unrelated Circles
10. A Sangaku by a Teen
11. A Sangaku Follow-Up on an Archimedes' Lemma
12. A Sangaku with an Egyptian Attachment
13. A Sangaku with Many Circles and Some
14. An Old Japanese Theorem
15. Archimedes Twins in the Edo Period
16. Arithmetic Mean Sangaku
17. Bottema Shatters Japan's Seclusion
18. Circles and Semicircles in Rectangle
19. Circles in a Circular Segment
20. Circles Lined on the Legs of a Right Triangle
21. Equal Incircles Theorem
22. Equilateral Triangle, Straight Line and Tangent Circles
23. Equilateral Triangles and Incircles in a Square
24. Five Incircles in a Square
25. Four Hinged Squares
26. Four Incircles in Equilateral Triangle
27. Gion Shrine Problem
28. Harmonic Mean Sangaku
29. Heron's Problem
30. In the Wasan Spirit
31. Incenters in Cyclic Quadrilateral
32. Japanese Art and Mathematics
33. Malfatti's Problem
34. Maximal Properties of the Pythagorean Relation
35. Neuberg Sangaku
36. Out of Pentagon Sangaku
37. Peacock Tail Sangaku
38. Pentagon Proportions Sangaku
39. Pythagoras and Vecten Break Japan's Isolation
40. Radius of a Circle by Paper Folding
41. Review of Sacred Mathematics
42. Sangaku ŕ la V. Thebault
43. Sangaku and The Egyptian Triangle
44. Sangaku in a Square
45. Sangaku Iterations, Is it Wasan?
46. Sangaku with 8 Circles
47. Sangaku with Three Mixtilinear Circles
48. Sangaku with Versines
49. Sangakus with a Mixtilinear Circle
50. Sequences of Touching Circles
51. Square and Circle in a Gothic Cupola
52. Tangent Circles and an Isosceles Triangle
53. The Squinting Eyes Theorem
54. Steiner's Sangaku
55. Three Incircles In a Right Triangle
56. Three Squares and Two Ellipses
57. Three Tangent Circles Sangaku
58. Triangles, Squares and Areas from Temple Geometry
59. Two Arbelos, Two Chains
60. Two Circles in an Angle

Copyright © 1996-2008 Alexander Bogomolny