Inversion: Reflection in a Circle

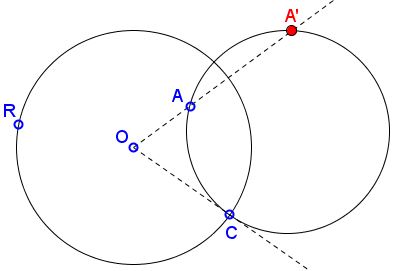
Let there be a circle t with center O and radius R. (In the applet, R also denotes a draggable point on the circle, such that OR is the radius of the circle.) And let there be a point A that could be located anywhere in the plane, except the center O. There is a whole bunch of circles that pass through A and that a perpendicular to t. C is one of the points -- the one that could be dragged -- where the given circle and that through A intersect. The applet suggests the following statement:

The situation is quite reminescent of reflection in a line. Two points A and A' symmetric in a straight line lie at equal distances to the line on a perpendicular to that line. Therefore, any circle with center on the line that passes through one of the points passes necessarily through the other. These are the circles perpendicular to the line. Our statement is obtained if the word "line" is replaced with the word "circle".

The prove of the statement is simple. Let g be a circle that passes through A and is perpendicular to t. Let A' be a second point of intersection of OA with g. Then OC is tangent to g. Therefore

The latter implies that the location of point A' does not depend on circle g. Indeed, A' lies on the line OA at distance equal to R²/OA. The point A' is known as the inverse (or inversion, or reflection) of A in t. From (1) it is obvious that if A' is the inverse of A, then A is the inverse of A', so that the points are said to be symmetric in the circle, or to be reflections of each other. A' is said to be the inverse image of A with respect to, or in, the given circle. Obviously, if A' is the inverse image of A, then A is the inverse image of A'.

Except of the center of t, which is known as the center of inversion, all points A in the plane have inverse images A'. The term inversion also applies to thus defined transformation of the plane. The transformation maps the points inside t to the points in its exterior, and vice versa. The points on t are fixed under that transformation, as are the circles perpendicular to it. The latter, of course, are not fixed pointwise. Lines through the center of inversion (with the exception of the center itself) also have that property. The curves that coincide with their own inverse are called anallagmatic.

(1) leads to an alternative, more algebraic, definition of inversion. R is known as the radius of inversion, R² as the power of inversion.