Chain of Inscribed Circles

Construct two tangent circles Σ₁ and Σ₂ and the line L through their centers. We are going to inscribe into the crescent-shaped space between the circles a chain of pairwise tangent circles. The first one, α₀, has its diameter on L. The second, α₁, is tangent to α₀, and both Σ₁ and Σ₂, and so on. Let h_n and R_n denote the distance to L from the center and the radius of the circle α_n. Then

(1) h_n = 2n·R_n.

If you are reading this, your browser is not set to run Java applets. Try IE11 or Safari and declare the site https://www.cut-the-knot.org as trusted in the Java setup.

What if applet does not run?

Indeed, an inversion with the center at the common point of tangency of Σ₁ and Σ₂ maps the two circles onto two parallel lines perpendicular to L. The circles α_n map an a chain of equal circles inscribed between the two parallel lines with the diameter of the first one on L. For those circles, the analogue of (1) is obvious: h'_n = 2n·R'_n, where h'_n is the distance from the center of the inverse image of α_n to L and R'_n is its radius. However, the circles in every inverse pair are homothetic with the center of homothety at the center of inversion. Let d_n and d'_n be the distances from the center of inversion to the centers of circle α_n and its inverse image. Then comparing the similar triangles formed by their line of centers and the common tangent gives a proportion

d_n/R_n = d'_n/R'_n.

Now looking ad the second pair of similar triangles, viz., those formed by the center line and the horizontal axis we get

h_n/d_n = h'_n/d'_n.

Whence, h_n/R_n = h'_n/R'_n = 2n.

(The above proposition is commonly referred to as Pappus Circle Theorem or Pappus Chain Theorem. Pappus was of course unaware of the inversion. His proof is much more elaborate. He himself refers to it as "The Ancient Theorem" [Gaba].)

We can easily derive an additional result.

Assume the radius of the right semicircle is k times the radius of the left one. If the former is R_R, and the latter is R_L, we assume that

(2) R_R = k·R_L.

Let R denote the radius of the big semicircle, then, since R = R_R + R_L, (2) implies that

(3) R_L = R/(1 + k) and
R_R = R·k/(1 + k).

For the sake of simplicity, let's choose the radius of the circle of inversion to be 2R. Then the left vertical line (this is the one that corresponds to the big semicircle) becomes tangent to both the big and the right semicircles as the common point of tangency lies then on the circle of inversion and is thus fixed. The right vertical line corresponds to the left semicricles. Introduce further notations. Let O_n be the center of a_n and P_n the projection of O_n on L. Let AB, CB, and AC denote the diameters of the semicircles. 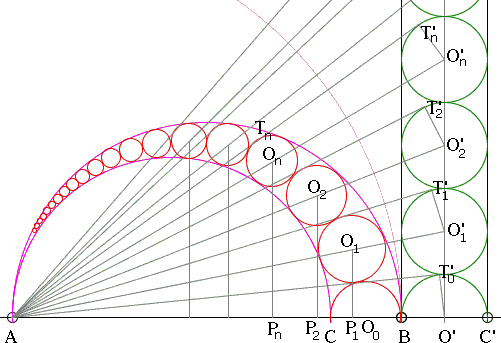A is the center of inversion, AB = 2R, AC = 2R_L, CB = 2R_R, C' is the inversion of C, O' is the midpoint of BC'.

(2R)² = AB² = AC·AC'.

Thus

AC' = (2R)²/AC = 4R²/2R_L = 2(1 + k)R.

And, since AO' = (AB + AC')/2,

AO' = (2 + k)R,
BO' = kR.

So, for the same reason as (1),

h_n/AP_n = 2nBO'/AO', or
R_n/AP_n = BO'/AO'

And

(4) AP_n = AO'·R_n/BO' = (2 + k)R_n/k.

Next, let's derive a generalization of Archimedes' formula:

(5) R_n = Rk / (k²n² + k + 1).

The points of tangency of the common tangents through A of a pair of corresponding circles (like T_n and T'_n in the diagram) play a double role. On one hand, they are homologuous, corresponding under the implied homothety. On the other hand, they are antihomologous, mapping on each other under the inversion. More accurately

AT'_n / AT_n = R'_n / R_n = Rk / R_n, and also
AT'_n · AT_n = (2R)²

implying

(AT'_n)² = 4R³k / R_n.

But (AT'_n)² = (2R + kR)² + (2n·kR)² - (kR)² which gives an equation for R_n, with the solution

R_n = Rk / (n²k² + k + 1).

which is (5). The combination of (4) and (5) gives

(6) AP_n = R(k + 2) / (k²n² + k + 1).

Note that, t = 1/k, so that R_L = t·R_R then (5) becomes

(5') R_n = Rt / (t² + t + n²).

References

M. G. Gaba, On a Generalization of the Arbelos, Am Math Monthly, Vol. 47, No. 1 (Jan., 1940), 19-24

Inversion - Introduction

72099676