Let's consider several examples.

For dist in the plane the sphere S(0, 0) is also a square but now its sides are parallel to the axes.

Observe that for a pair of points X and Y

dist(X, Y) ≤ dist2(X, Y) ≤ dist1(X, Y).

However, the unit spheres corresponding to the three distances are included in the reverse order. Why?

Thus it's clear that once several distance functions have been defined on the same set the expression "the distance between two points" becomes ambiguous. However, as is suggested by the spheres diagram above, points in R² "close" in one of the distances dist, dist₁, dist₂ will be close in the others. More accurately, the following is true:

Proposition

Let a sequence of plane points A, A₁, A₂, A₃, ... be such that dist_i(A, A_k)->0 as k goes to infinity for i being one of , 1, or 2. Then the same is true for the remaining values of i.

Proof

The Proposition follows from the following series of inequalities:

dist(X,Y) ≤ dist2(X, Y) ≤ dist1(X, Y) ≤ 2dist(X, Y)

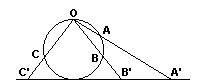
Now it's time to fulfill the implicit promise made at the beginning of the page. Consider what's known as the Stereographic projection. The name derives from a configuration in R³ but I'll use its 2-dimensional analog. A circle stands on a straight line. Through its North pole O and the points of the horizontal axis draw straight lines and note the points of intersection with the circle. So that points A,B,C from the circle correspond to the points A',B', and C' on the x-axis. This is a 1-1 correspondence between points of a straight line and points on a circle without its North pole. Let's define the distance on the latter set, S²-{North pole}, as dist_s(X, Y) = dist₂(X', Y'). Then it's clear that the points close in the angular dist_a may be far apart in the distance dist_s. To see this pick up points near to but on opposite sides of the pole.

The stereographic projection works both ways. So that the formula dist_r(X', Y') = dist_a(X, Y) defines a new distance function on R¹. It's easy to see that there are points on the axis distant in, say, dist₂ but close in dist_r.