Tangent Circles and an Isosceles Triangle II
Solution by Vladimir

The applet presents a solution to the following Sangaku problem: Given a circle S with center O and diameter AC and point B on AC. Form circle G with center P and diameter AB and an isosceles triangle BCE with E on the circle S. Circle W with center Q is inscribed in the curvilinear triangle formed by circles S and G and the line BE. Prove that QB is perpendicular to AC.

(Another solution appears elsewhere. The one below is remarkable in an absolute absence of calculations.)

What if applet does not run? -->

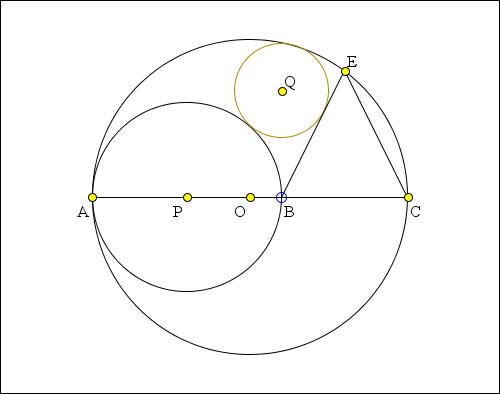
Reformulate the problem a little: (O), (P) are circles with diameters AC > AB tangent at A. Perpendicular bisector of BC cuts (O) at E, F, so that triangle BEC is isosceles (or BECF is a rhombus). Circle (Q) is internally / externally tangent to (O), (P) and to BE. Prove BQ is perpendicular to AC.

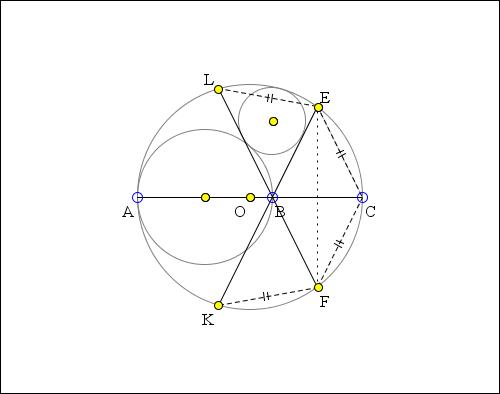
EB, FB cut (O) again at K, L. FE bisects angle ∠CFL = ∠CFB, implying EL = EC = EB so that B is the incenter of ΔCKL. Perpendicular to AC at B cuts (O) at M, N. By construction, (O) cuts circle (B) with center B and diameter MN in diametrically opposite points which means that the inversion in (B) with negative power -BM² takes (O) into itself.

Line EBK through the inversion center also goes to itself. Power of B to (O) is -BM² = BM × BN = BA × BC, meaning that the inversion takes A to C. Circle (P) with diameter AB goes to line perpendicular to AC at C, the external bisector of the angle ∠KCL.

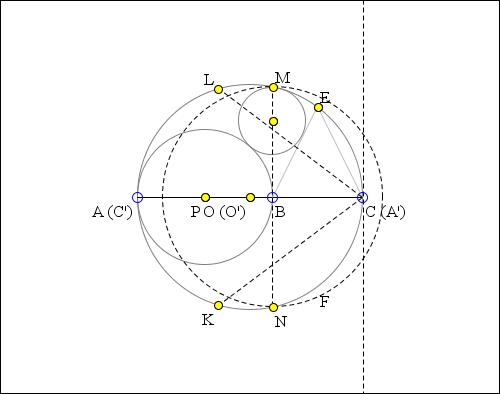
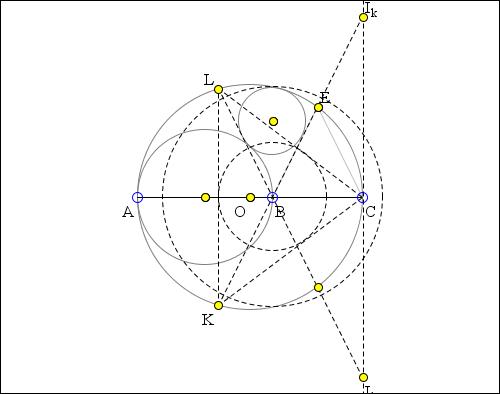
Let I_k, I_l be K-, L-excenters of ΔCKL. The inverse image (Q') of (Q) is tangent to I_kI_l, to BE = BI_k, and (by Feuerbach's Theorem) externally tangent to the 9-point circle (O) of the triangle BI_kI_l, therefore (Q') is its excircle in the angle BI_kI_l, centered on the external bisector of the angle EBF, i.e., the angle I_kBI_l, perpendicular to the internal bisector BC of this angle, therefore BQQ' is perpendicular to AC.

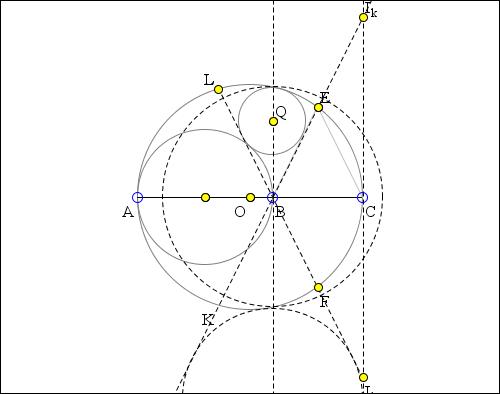
This permits generalization to a non-isosceles triangle CKL with circumcircle (O) and incenter B and angle bisector CBA. (P) is circle with diameter AB, (Q) is circle internally tangent to (O), externally tangent to (P), and to the angle bisector KBE. No change in the proof that (O) is also tangent to the other angle bisector LBF.

Another solution makes use of the common inversion.

Inversion - Introduction

• Angle Preservation Property
• Apollonian Circles Theorem
• Archimedes' Twin Circles and a Brother
• Bisectal Circle
• Chain of Inscribed Circles
• Circle Inscribed in a Circular Segment
• Circle Inversion: Reflection in a Circle
• Circle Inversion Tool
• Feuerbach's Theorem: a Proof
• Four Touching Circles
• Hart's Inversor
• Inversion in the Incircle
• Inversion with a Negative Power
• Miquel's Theorem for Circles
• Peaucellier Linkage
• Polar Circle
• Poles and Polars
• Ptolemy by Inversion
• Radical Axis of Circles Inscribed in a Circular Segment
• Steiner's porism
• Stereographic Projection and Inversion
• Tangent Circles and an Isosceles Triangle
• Tangent Circles and an Isosceles Triangle II
• Three Tangents, Three Secants
• Viviani by Inversion
• Simultaneous Diameters in Concurrent Circles
• An Euclidean Construction with Inversion
• Construction and Properties of Mixtilinear Incircles
• Two Quadruplets of Concyclic Points
• Seven and the Eighth Circle Theorem
• Invert Two Circles Into Equal Ones

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny