An Euclidean Construction with Inversion

Here is a problem from The Amewrican Mathematical Monthly (11572, v 120, February 2013, p 176-7). The problem was proposed by Sam Sakmar, University of South Florida, Tampa, FL

Given a circle \(C(O)\) and two points \(A\) and \(B\) outside \(C(O)\), give an Euclidean construction to find a point \(P\) on \(C(O)\) such that if \(Q\) and \(S\) are the second intersections with \(C(O)\) of \(AP\) and \(BP\) respectively, then \(QS\) is perpendicular to \(AB\). (Special configurations, including the case that \(A\), \(B\), and the center of \(C(O)\) are collinear, are excluded.)

The applet below serves a dynamic illustration:

Proof

Solution is by Robert A. Russel, New York, NY.

In general, the problem has two solutions. These are the two points of intersection of the given circle \(C(O)\) with the circle through \(A\) and \(B\) perpendicular to \(C(O)\).

How to construct such a circle? Inversion in circle \(C(O)\) preserves points on \(C(O)\), lines through its center \(O\), and the circles orthogonal to \(C(O)\). If \(C(F)\) is the circle through \(A\) and \(B\) orthogonal to \(C(O)\), then the imgages \(A'\) and \(B'\) of \(A\) and \(B\) lie on \(C(F)\). It follows that \(C(F)\) can be constructed as the circumcircle of, say, \(\Delta ABA'\).

Let \(P\) be one of the intersections of the two circles. (The proof refers to the following diagram.)

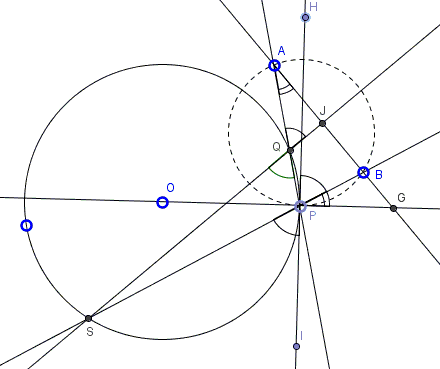
a geometry problem from The American Mathematical Monthly, February 2013

In the diagram there are several auxiliary points: \(G\) is the intersectio of \(AB\) and \(OP\); \(J\) the intersection of \(AB\) and \(SQ\); \(I\) and \(H\) are points \(FP\) on two sides from \(P\). On the other hand, the center \(F\) of the constructed circle is not shown. Since the two circles are orthogonal, \(OP\perp FP\) and \(OP\) is tangent to \(C(F)\) whereas \(FP\) is tangent to \(C(O)\). We thus can use the properties of inscribed angles and angles formed by a tangent and a chord.

Observe that

\( \angle BPG=\angle BAP =\angle JAQ \)

and

\( \angle BPH=\angle IPS =\angle PQS=\angle AQJ, \)

Now \(\angle BPH+\angle BPG=\angle GPH = 90^{\circ}\). It follows that also \(\angle JAQ+\angle AQJ= 90^{\circ}\). Therefore, in \(\Delta AJQ\), \(\angle AJQ=90^{\circ}\), as required.

Inversion - Introduction

71871238