Inversion in the Incircle
What Is It About?
A Mathematical Droodle
| Buy this applet What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2015 Alexander Bogomolny
Inversion in the Incircle
The applet suggests the following theorem [Mathematical Gems II]:
The inverse images of the side lines of a triangle in its incircle are three circles of equal radii that concur at the incenter. The circle through their second points of intersection is none other than the inverse image of the circumcircle. It has the same radius.
| Buy this applet What if applet does not run? |
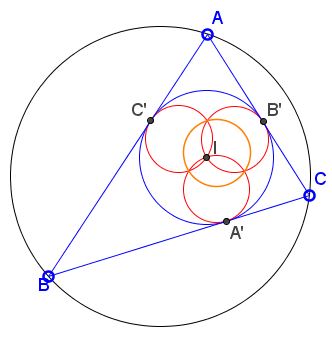
R. Honsberger credits Arnold Emch (1916) with the following observation.
For a given ΔABC, we are interested in the inversion in its incircle. The side lines (being tangent to the incircle) invert into the circles that pass through the incenter (I) and still tangent to the side lines at the same points (A', B', C') of tangency, as the side lines. These circles have IA', IB', and IC' as their diameters. The three are therefore equal.
Their second points of intersection correspond by the inversion to the vertices of ΔABC. It follows that the circle through these three points is the inverse image of the circumcircle of ΔABC. As we know, it has the same diameter as the other three circles, viz., r - the inradius of ΔABC. We have obtained a nice result:
Under inversion in the incircle of a triangle, the side lines and the circumcircle are carried into four equal circles with the common diameter equal to the inradius of ΔABC.
References
- R. Honsberger, Mathematical Gems II, MAA, 1976, pp. 20-21
Corollary
Nathan Bowler has noticed that the above configuration yields a simple proof of the well known identity (yet another Euler's formula):
| (*) | OI2 = R2 - 2Rr, |
where R and r are the circumradius and the inradius of ΔABC.
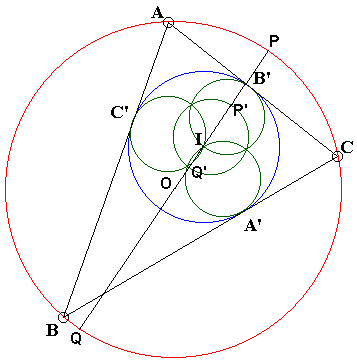
Let P and Q be the two points of intersection of OI with the circumcircle, such that
IP = R - OI and IQ = R + OI.
Let P' and Q' be the inverses of P and Q, respectively. Then, since P'Q' is the diameter of the inverse image of the circumcircle,
IP' + IQ' = r.
Now we have
| r | = IP' + IQ' |
| = r2/IP + r2/IQ | |
| = r2/(R - OI) + r2/(R + OI) | |
| = r2·2R / (R2 - OI2), |
which simplifies to
R2 - OI2 = 2Rr.
The latter is equivalent to (*) and conventionally appears in the following form
1 / (R - OI) + 1 / (R + OI) = 1 / r.
It is a curious fact that the inverse image of the circumcircle in the incircle is the 9-point circle of ΔA'B'C', from which, too, we see that its diameter is equal to the inradius of ΔABC.
Inversion - Introduction
- Angle Preservation Property
- Apollonian Circles Theorem
- Archimedes' Twin Circles and a Brother
- Bisectal Circle
- Chain of Inscribed Circles
- Circle Inscribed in a Circular Segment
- Circle Inversion: Reflection in a Circle
- Circle Inversion Tool
- Feuerbach's Theorem: a Proof
- Four Touching Circles
- Hart's Inversor
- Inversion in the Incircle
- Inversion with a Negative Power
- Miquel's Theorem for Circles
- Peaucellier Linkage
- Polar Circle
- Poles and Polars
- Ptolemy by Inversion
- Radical Axis of Circles Inscribed in a Circular Segment
- Steiner's porism
- Stereographic Projection and Inversion
- Tangent Circles and an Isosceles Triangle
- Tangent Circles and an Isosceles Triangle II
- Three Tangents, Three Secants
- Viviani by Inversion
- Simultaneous Diameters in Concurrent Circles
- An Euclidean Construction with Inversion
- Construction and Properties of Mixtilinear Incircles
- Two Quadruplets of Concyclic Points
- Seven and the Eighth Circle Theorem
- Invert Two Circles Into Equal Ones
Nine Point Circle
- Nine Point Circle: an Elementary Proof
- Feuerbach's Theorem
- Feuerbach's Theorem: a Proof
- Four 9-Point Circles in a Quadrilateral
- Four Triangles, One Circle
- Hart Circle
- Incidence in Feuerbach's Theorem
- Six Point Circle
- Nine Point Circle
- 6 to 9 Point Circle
- Six Concyclic Points II
- Bevan's Point and Theorem
- Another Property of the 9-Point Circle
- Concurrence of Ten Nine-Point Circles
- Garcia-Feuerbach Collinearity
3 Equal and Concurrent Circles
- Johnson Circles
- Three equal circles
- 3 circles having the same radius
- Inversionn in the Incircle
- Orthocenter and Three Equal Circles
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2015 Alexander Bogomolny
| 49551999 |
