Angle Preservation Property

Circles that do not pass through the center of inversion are inverted into circles. Any two circles could be inverted into one another. Indeed, any center of homothety of the two circles could be used as the center of inversion. The points that correspond to each other under homothety are called homologous. The points that correspond to each other under inversion are antihomologous. For example, in the diagram below the points in the pairs A, B' and A', B are homologous, whereas A, A' and B, B' are antihomologous.

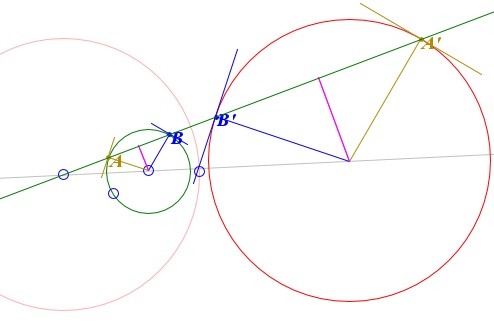
angle are preserved under inversion

Because of this connection between inversion and homothety, inversion, as does homothety, enjoys the angle preservation property: under inversion angles do not change. There are other ways to describe that property. In complex analysis, mappings that preserve angles are called conformal, in geometry they are said to be isogonal.

A caveat is in order. Both definitions of inversion leave out the center of inversion that does not correspond to any point. It is customary to complement the definitions by assigning the point at infinity to the center of inversion (and vice versa, of course.) This is not the same infinity as that shared by all parallel lines, rather every straight line closes on itself at the "new" infinity. The straight lines thus may be (and are in inversive geometry) looked at as circles with center at infinity and an infinite radius. The angle preservation property means in particular that two circles tangent at the center of inversion are mapped onto two parallel lines. Two circles that cross at the center of inversion are mapped onto two intersecting straight lines.

Assume under the inversion in a circle with radius R points P and Q map onto the points P' and Q', respectively. Then triangles OPQ and OQ'P' are similar. Indeed, the angles at O coincide and, in addition, OP/OQ' = OQ/OP' (for, OP·OP' = OQ·OQ' = R².) It follows that PQ/P'Q' = OP/OQ', or

(1)	P'Q' = R²·PQ/(OP·OQ)

If the inversion is followed by a reflection, i.e. if we consider an inversion with a negative power k, the formula (1) changes only slightly:

(2)	P'Q' = \|k\|·PQ/(OP·OQ),

which holds regardless of the sign of the power of inversion. (2) is a general formula that relates the distance between two points to the distance between their inverse images.

Inversion - Introduction

72104249