In a few words...

While putting together these pages I sometimes feel a need to refer to a term without straying from the topic at hand. Oftentimes it's possible to locate a resource on Internet with a necessary definition but cumbersome to specify the reference. In short, I decided to maintain a page of very short topical descriptions which, if and when a need or inspiration induce me to, I'd be able to expand upon.

Many of these have been mentioned on the Did you know... page where, as a group, they, I hope, provided some entertainment. As I had neither immediate need for nor intention to describe them, some terms from that page have been left dangling without any reference or definition.

Hence the current page.

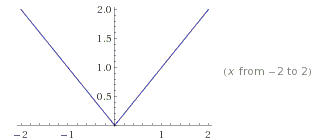
• Absolute value.
  The absolute value is defined for real and complex numbers. For real numbers, the absolute value coincides with the number itself if the latter is either positive or zero. The absolute value of a negative number is obtained by multiplying the number by -1, i.e. by changing its sign. The absolute value of a number r is denoted |r|. Therefore, |r| = r for r ≥ 0 and |r| = -r for negative r. In other words, |r| is the distance from number r to the origin. In this form, the definition applies to complex numbers that are identified with points in the plane.

• Algorithm.
  The word algorithm comes from the name of a Persian author, Abu Ja'far Mohammed ibn al Khowarizmi (circa 825) who wrote a math textbook. (Incidently, he also wrote a book on the Hebrew calendar.) The word refers to a precise prescription (given by a step-by-step description) of a solution to a problem. (See also What Is Algorithm?)

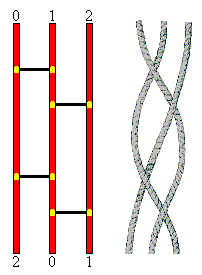
• Braids Theory.
  Braids Theory was invented by Emil Artin and is a part of the Knot Theory. Braids are collections of lines whose ends are attached to two parallel straight lines. There is an interesting puzzle related to the Braids Theory.

• Cardinal.
  Cardinal numbers were invented by Georg Cantor and generalize the notion of a number of elements to infinite sets. Finite cardinals are just regular non-negative integers. Transfinite cardinals are (often) defined as collections (equivalency classes) of sets that could be put into a 1-1 correspondence with each other. ℵ₀ is the first transfinite cardinal and describes the cardinality of denumerable sets, i.e. sets that can be put into a 1-1 correspondence with the set of all positive integers. (See a more extensive article on Cardinals.)

• Cardioid.
  A special case of epicycloids. A plane curve traced by a point on a circle rolling on the outside of a circle of equal radius.

• Cartesian coordinates.
  Most often in the plane, but also in the higher dimension spaces, the Cartesian coordinates are defined by a number (2 in the plane) of perpendicular number lines - coordinate axes. A point is then defined by its projections on the axes. In the plane, points are defined by 2 such projections that are written as an ordered pair of real numbers, (x, y).

• Cauchy sequence.
  A sequence x₀, x₁, ... of elements of a metric space is said to be a Cauchy sequence if differences |x_n+m - x_n| are uniformly small in m (i.e. do not depend on m) and tend to 0 as n grows.

• Circle.
  A circle is a geometric shape - a set of points - consisting of points equidistant from a given point, the center of the circle. The common distance of the points on the circle to its distance is called the radius of the circle. (See a more detailed account.)

• Circumference.
  Circumference is a number, usually the length of a circle, which is a geometric figure. "The circumference of a circle" is a meaningful expression, while "cut the circumference of a circle in two points" is not. Regretfully, the usage is wide spread: the word "circumference" is often used as a substitute for the word "circle".

• Closed interval.
  Closed interval is a piece of a straight line that includes its endpoints. On the number line, closed intervals [a, b] are defined as {x: a ≤ x ≤ b}. Closed intervals are closed sets.

• Complementary angles.
  Two angles are called complementary is they add up to 90°. E.g. two acute angles in a right triangle are complementary.

• Completeness.
  There are at least three distinct notions of completeness.

  • Axiomatic completeness.
    An axiomatic theory is complete if every syntactically correct statement in the theory can be proven either right or wrong.

  • Graph's completeness.
    A graph is complete if any two of its vertices are connected by exactly one edge. A complete graph with N vertices is often denoted as K_N.

  • Metric completeness.
    A metric space is complete if all Cauchy sequences of its elements converge.

• Concentric.
  Concentric means having a common center. The term may apply to other objects, but most often and most naturally it applies to two circles.

• Cone.
  The term cone appears in at least two contexts.
  
  

  • In geometry, a cone is formed by a family of straight lines through the same point tracing a (commonly planar) curve. The point is called the apex or vertex of the cone.

  • In functional analysis, a cone is defined for an ordered set and consists of all elements that exceed a given one.

• Connected set.
  A set that can't be split into a union of two sets each of which is both open and closed.

• Consistency.
  An axiomatic theory is consistent if it's impossible (in the confines of the theory) to prove simultaneously a statement and its negation. The Godel's Theorem states that any (sufficiently powerful) consistent axiomatic theory is incomplete.

• Continuity.
  A mapping f:A->B is continuous if images f(a₁) and f(a₂) of two close points a₁ and a₂ are also close to each other. This is only meaningful if for both spaces A and B the notion of closeness has been defined. The latter is defined in terms of neighborhoods.

• Continuum.
  Any set that may be brought into 1-1 correspondence with the set of real numbers. Examples: a finite line segment, a square, a circle, a disk. Also, the cardinality of all such sets which is usually denoted c or a Gothic c, which I can't reproduce.

• Coprime.
  Two integers n and m with no common factors are said to be mutually prime or coprime. By definition, gcd(n, m) = 1.

• Curve.
  A curve is a continuous mapping of the segment [0, 1] into another space - container of the curve. A curve may not look as a line. For example, there are space filling curves.

• Data structure.
  Data structure is both a programming language construct that unifies several related attributes and a basic data type. Realization of the utility of data structures in programming led eventually to the modern object oriented trend. Among the basic data types are the stack, list, queue, tree.

• Diameter.
  The word Diameter has several meanings in mathematics. For a circle, diameter is either the line inside the circle through its center, or the length of such a line. As a number, the diameter is twice the radius of the circle. As a line segment, a diameter joins two points on the circle lying opposite each other. All diameters of a circle meet in its center. The definition of diameter as a line segment in a circle extends to arbitrary convex shapes and triangulations.

• Equation.
  An equation is a statement that two mathematical object, e.g. algebraic expressions, are equal under certain conditions. Equations are usually and sometimes tacitly accompanied by the requirement to establish these conditions. In the case where mathematical objects contain arbitrary variables, such a requirement may mean finding those values of the variables that turn the equation into equality. Equations are written as two mathematical objects connected by the equality sign "=". Equations are sometimes called more explicitly as conditional equations.

• Equality.
  An equality is a statement of two mathematical objects being equal. Like equations, equalities are written as two mathematical objects connected by the equality sign "=". The meaning of two objects being equal depends very much on the nature of the objects. E.g., two matrices are equal iff they have identical dimensions and all their corresponding elements are equal. Two triangles are equal if there exists a distance preserving transformation that maps one on the other (Nowadays equal triangles more often than not are called congruent.) Equalities are sometimes called unconditional equations.

• Extreme value, local or global.
  A function f: A -> B is numeric if B is a set of numbers. For a numeric function it's possible to compare its values at different points aA. Extreme is a value which, in some sense is either maximum or minimum. If f(a) exceeds all other values of f then we say it's a global extreme, maximum. If it's only larger than values of f for points near a, the maximum is local.

• Field.
  A field is a ring in which multiplication is a group operation. In France (and sometimes elsewhere in Europe), the multiplicative group need not be commutative. In the US and Russia it must be.

• Floor.
  For a real number r, its floor value [r] is defined as the largest integer not greater than r. Thus [5] = [5.1] = 5 and [-5] = -5 while [-5.1] = -6.

• Fractional Part.
  For a real number r, its fractional part is defined as {r} = r - [r], where [r] is the floor value of r.

• Free group.
  Groups have generators, such elements that all other elements of a group could be obtained from generators and their inverses using the group operation. A group is said to be free if no relation exists between its generators other than between an element and its inverse. The additive group of integers is free with a single generator 1. The multiplicative group of all positive rational numbers has prime numbers as its generators. From the Fundamental Theorem of Arithmetic representation of integers in the form p^aq^b...r^c where p, q, ..., r are all different primes, is unique. Therefore the group is free. The group of sliding motions in the sliders puzzle is not free. Indeed, for the sequence S_j+S_+iS_j-S_-i we obviously have the following identity (S_j+S_+iS_j-S_-i)³ = Id, where Id is the unit element of the group, i.e. the element that leaves all the counters unchanged.

• Game Theory.
  The Game Theory studies winning strategies for parties involved in situations where their interest conflict with each other. Developed by John von Neumann, the theory has applications to real games (cards, chess, etc.), economics, commerce, politics and some say even military. J. Conway used his theory of surreal numbers to qualitatively evaluate game positions. Conway wrote: It's especially delightful when you find a game that somebody's already considered and possibly not made much headway with, and you find you can just turn on one of these automatic theories and work out the value of something and say, "Ah! Right is 47/64ths of a move ahead, and so she wins."

• Gradient.
  Gradient is a vector pointing in the direction of the maximal change of a function of two or more variables. Components of the gradient of a function in Cartesian coordinates are just partial derivatives of that function. In 2-dimensional space, the gradient is often confused with the slope of the graph of a function of one variable. Given a function y = f(x), it is always possible to look at its graph as 0-level curve of function F(x, y) = f(x) - y. In this case, the gradient of F, grad(F), is the vector (f'(x), -1), with the first component being the derivative of f(x) - read "the slope of the graph of y = f(x)." Thus the notions of the slope and that of the gradient are related. However, one of them is a scalar (slope), the other a vector (gradient).

• Group.
  Group is the most fundamental and pervasive notion of the Higher or Abstract Algebra. It's a set along with a single operation defined on its elements. The group is called additive if the symbol for the operation is "+". It's multiplicative if the symbol "·" of multiplication is used instead. But any other symbol can be used as well. There is always a unique element (1, for multiplicative, and 0, for additive, groups) that leaves elements invariant (unchanged) under the defined operation, like a + 0 = a. Also, for every element a there exists a unique inverse b such that, for example, in the case of the additive symbol, a + b = 0 and b + a = 0. Most often, however, the inverse is denoted as a^-1. Lastly, the group operation must be associative like in a·(b·c) = (a·b)·c. A group is commutative or Abelian if its operation is symmetric, like in a + b = b + a.

• Growth.
  Many things may grow in Mathematics. Functions may be monotone or grow in jumps. Complexity of a system may grow exponentially with the system size. Lately, due to the development of the Fractal Geometry, growth of crystals and other natural phenomena became a subject of scientific scrutiny.

• Heredity.
  A property of a space is hereditary if each of its subspaces possesses this property. Being countable is a hereditary property. Having holes is not.

• Hole.
  Torus has a hole; sphere does not. If every curve on a surface can be continuously shrunk into a point the surface has no holes. Attaching handles to the sphere in order to create surfaces with holes is an important and ubiquitous topological activity.

• Ideal.
  The word ideal appears in Mathematics in at least a couple of contexts.

  • Ideal elements.
    In Geometry it's often a convenience to introduce a point at infinity as an ideal (probably too good to be real) element. Completion of a metric space by incorporating ideal elements which are limits of Cauchy sequences results in a complete metric space.

  • Ideal subrings.
    Subrings of a ring are its subsets which are rings in their own right. For a given ring R, its subring I is (an) ideal if for every rR and iI both r·i and i·r belong to I. For an ideal I it's possible to define a factor ring R/I.

• iff.
  An abbreviation which stands for if and only if.

• Infinitesimal.
  In common calculus infinitesimal is a variable whose limit is zero. In the non-standard analysis developed by Abraham Robinson (1960) infinitesimal is a quantity whose absolute value is less than that of any real number. Infinitesimals have been widely (and uncritically) used by the creators and the pioneers of calculus. Non-standard analysis supplied a fundamental justification for their genius.

• Infinity.
  Infinity pops up in a variety of places. A function may grow to infinity when it's not bounded from above. In Geometry, it's often convenient to think of parallel lines as intersecting at a point at infinity. G. Cantor was the first to introduce and systematically study various kinds of infinities.

• Integer.
  This is a very basic notion. To define it rigorously we may need a set of axioms, like those proposed by G.Peano. Usually, integers are numbers from the sequence ..., -2, -1, 0, 1, 2, ..., positive members of which are often called counting or natural numbers. Sometimes, 0 is also judged to be natural. For a long time, I used the word integer (not quite conventionally) to mostly designate the counting numbers. The reason is that this is the set used most frequently. So it's appropriate to denote it with the shorter word: "integers" instead of "counting numbers". More recently, I tried to bring the site's terminology more in agreement with the common use. I'd be grateful for pointers to any remaining incosistencies.

• Jump.
  A function has a jump at a point where its limits from right and left both exist but do not coincide.

• Law of excluded middle.
  One of the two: either a statement is true or it is false. There's nothing in-between. An axiom of 2-valued logic.
  

• Model.
  Kepler and Newton laws are models of the real world. These are very good models due to their predictive power. Mathematical biologists derive equations (create models) of population growth and spread of epidemics. Mathematical economist create models that describe some aspects of and help study real world economy. Modeling being so important, there is of course the Model Theory. It's a general theory of interpretations of axiomatic systems. A hyperbolic (non-euclidean) geometry can be modeled in a circle of the regular euclidean geometry. This implies independence of the Axiom of Parallels (the Fifth Postulate) from the rest of the euclidean axioms.

• Multiplicand.
  A quantity multiplied by another. A product is obtained by multiplying two or more multiplicands.

• Neighborhood.
  (Set-theoretical) topology starts with a definition of open sets which are often and interchangeably called neighborhoods. By definition, the empty set is open and so are finite intersections and arbitrary unions of open sets. A set is a topological space if some of its subsets are declared to be open subject to these conditions. An open set is a neighborhood of all its points. A function f: A -> B from one topological space into another is continuous at a point aA if for every neighborhood V of f(a) there exists a neighborhood U of a such that f(U)V. This is equivalent to saying that inverse images of sets open in B are open in A. Complements of open sets are closed by definition.

• Numeral.
  Numeral is a written symbol that denotes a number. People did not always use numerals even after learning to write. A symbol for 0 came into use only in the last millennium.

• Open interval.
  Open interval is a piece of a straight line that does not contain the endpoints. On the number line, open intervals (a, b) are defined as {x: a < x < b}. Open intervals are open sets.

• Paradox.
  The Greek philosopher Zeno (circa 460 BC) is famous for several paradoxes. In one Achilles couldn't catch a tortoise because he had first to reach the point where the tortoise started. Meanwhile, the tortoise would move to another point, etc. B. Russell has discovered paradoxes of infinity (The set of all sets that do not contain themselves - does it contain itself?) There are semantic paradoxes (All Web page authors are liars) and self-referential ones.

• Parity.
  The word parity applies to situations where two items or their properties may be juxtaposed as being opposites (in a certain context) of each other. Integers are of either odd or even parity when they are, respectively, odd or even. The convenience is in being able to say "two numbers of different parities" without having to explicitly mention which is which.

• Point.
  A point in an axiomatic geometry is an undefined basic term. In analytic geometry, a point in a plane is defined as an ordered pair of two (real) numbers. In higher dimension space, say, Rⁿ, a point is an n-tuple (x₁, x₂, ..., x_n).

• Pole.
  

  • A pole is a singularity of an analytic function where it behaves very nearly like a rational function. If the function is bounded around a singularity the latter is called removable.

  • A pole is a point that, in the presence of an angle, is paired with a straight line - its polar with respect to the angle.

  • A pole is a point that, in the presence of a circle, is paired with a straight line - its polar with respect to the circle.

  • A pole is a point that, in the presence of a triangle, is paired with a straight line - its polar with respect to the triangle.

• Program.
  A program is a sequence of instructions that accomplish a certain task. Often instructions are written in a machine language so that a computer may perform the task required.

• Projection.
  Our shadow is our projection on the ground. x is the projection on the X axis and y is the projection on the Y axis, of the point (x, y).

• Ring.
  A ring is an additive commutative group in which a second operation (normally considered as multiplication) is also defined. The multiplication must be associative, i.e. a + (b + c) = (a + b) + c and the distributive law a(b + c) = ab + ac and (b + c)a = ba + ca must hold. If a ring is also a commutative multiplicative group (of course, with 0 removed) then it's called a field.

• Set.
  The notion of a set is the most fundamental in Mathematics. Careless use of sets leads to contradictions the most famous of which was discovered by Bertrand Russell. Without going into details, sets are collections of elements that share some property P - the characteristic property of a set. The following notation is quite common: {x: P(x)} is read "the set of all x that have the property P". In view of the possibility of paradoxes, it must be remarked that not every possible property P defines a set.

• Similarity.
  Two triangles are similar if they have equal angles in which case their corresponding sides, say, a₁, b₁, c₁ and a₂, b₂, c₂, are proportional with a coefficient r: a₁/a₂ = b₁/b₂ = c₁/c₂ = r. Since side length could be looked at as the distances between the vertices, going from one triangle to another modifies these distances by a factor of r. Distances between other corresponding points in the triangles also change by the factor of r. This can be generalized. A similarity is such a transformation of the plane under which distance between any pair of points changes by the same factor. Similarity transformations play a central role in the Fractal Geometry and even more so in the theory of Iteration Function Systems (IFS). Consecutive Peano curves each consist of four images of itself each half the size of the whole. Similarity transformations are easily defined in spaces of higher dimensions.

• Slope.
  For a straight line in the plane, the slope is the tangent of the angle it forms with the positive X axis. For a curve (e.g., a graph of a function), the slope is, by definition, the slope of the tangent line. Therefore, if the slope is constant a line is straight. Slope being a number should not be confused with a related notion of gradient, which is a vector.

• Space.
  There are too many different spaces in Mathematics to enumerate all. Generally, space is a set of points with additional features.

  • Affine space.
    The best known example of the affine space is the plane although a straight line is another example. One important feature of affine spaces is the ability to fix a point and coordinate axes through it so that every point in the space can be represented as a tuple of its coordinates. Every (ordered) pair of points A and B in an affine spaces is associated with a vector AB, A being the beginning while B the end point of AB. For any three points A, B, C the following holds AB+BC+CA=0.

  • Linear space.
    Linear (often Vector) space is a collection of vectors which means that the space is an additive Abelian group and, in addition, its elements can be multiplied by scalars, i.e. elements of a field; for example, a field of real numbers.

  • Metric space.
    A space X is metric if there is defined a real non-negative function (metric, or metric function) of two variables d(A, B). The function is known as the distance between the two points. It's characterized by the following properties. For AX, BX, and CX

    1. d(A, B) = 0 if and only if A = B. (the distance is 0 if and only if the points coincide)

    2. d(A, B) = d(B, A) (the distance from A to B is the same as the distance from B to A)

    3. d(A, B) + d(B, C) ≥ d(A, C)(the sum of two sides of a triangle is never less than the third side.)

    There are many examples of distance functions.

  • Topological space.
    In a topological space every point has a collection of neighborhoods to which it belongs.

• Stability.
  Solution to a problem is stable if a small modification in the conditions of the problem does not change the solution too much. How much is much depends of course on the problem.

• Straight line.
  A straight line in an axiomatic geometry is an undefined basic term. In analytic geometry, a straight line is a set of points satisfying a linear equation.

• Subgroup.
  A subset H of a group G is a subgroup (of G) provided it's a group with respect to the group operation of G.

• Tree.
  

  • Trees, as special graphs, consist of nodes and edges and are best defined recursively. For every tree one node is singled out and is called the root. One node constitutes a tree and, naturally, is that tree's root. A collection of more than one node is a tree if by removing the root the remaining nodes fall into disjoint trees. Nodes connected to a tree root are called siblings.

  • A shorter way is to define the tree as a connected graph with no circuits. The absence of circuits means that there is always exactly one way to get from one vertex of the tree to any other.

  • As a basic data structure, tree is designed to easily store information about graph trees. In its commonest form a tree structure has pointers to the next sibling and the first child.

• Value.
  A function f: A->B is defined in A and takes values in B. Thus, for aA (a in A), f takes on the value of f(a)B.

• Whole number.
  

  Numbers ..., -3, -2, -1, 0, 1, 2, 3, ... are said to be integers, numbers 0, 1, 2, 3, 4, ... are called whole numbers, numbers 1, 2, 3, ... are the counting numbers.

Copyright © 1996-2009 Alexander Bogomolny