Two Quadruplets of Concyclic Points
What Might This Be About?
Problem
Four circles $S_1,$ $S_2,$ $S_3,$ $S_4$ cross pairwise: $S_1\cap S_2=\{A_1,B_1\},$ $S_2\cap S_3=\{A_2,B_2\},$ $S_3\cap S_4=\{A_3,B_3\},$ $S_4\cap S_1=\{A_4,B_4\}.$ Assume points $A_i,\space n=1,2,3,4$ are concyclic.
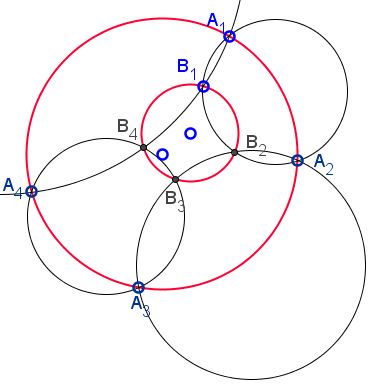
Then points points $A_i,\space n=1,2,3,4$ are also concyclic. (The circles involved may have infinite radius, i.e. be straight lines.)
Solution
The problem admits an equivalent formulation:
Given six points, $A_1,$ $A_3,$ $B_4,$ $B_3,$ $B_1,$ $A_2,$ assume that the circumcircles $(A_1A_2A_3),$ $(A_3B_3B_4),$ $(A_1B_1B_4)$ concur at point $A_4.$

Prove that the circumcircles $(A_1A_2B_1),$ $(A_2A_3B_3),$ $(B_1B_3B_4)$ concur at point $B_2.$
But this is Miquel's theorem for circles.
Acknowledgment
This is problem 217b from I. M. Yaglom's Geometric Transformations, v II, Russian original (1956). I'd guess that it is also included in a relatively late (2009) translation Geometric Transformations IV, but I do not have the book.
A more elementary solution has been placed on a separate page.
A Second Look
The problem could be approached differently (I change notation):
Given two quadruplets of concyclic points $\{A_i\}$, $\{B_i\},$ $i=1,2,3,4'$ It is known that points $A_1,B_1,B_2,A_2$ are concyclic and so are points $A_2,B_2,B_3,A_3$ and $A_3,B_3,B_4,A_4.$ Prove that points $A_4,B_4,B_1,A_1$ are also concyclic.
In this formulation the problem admits a generalization:
Given two sets of $n$ concyclic points each $\{A_i\}$, $\{B_i\},$ $i=1,\ldots,n,$ where n is an even integer. It is known that points $A_i,B_i,B_{i+1},A_{i+1}$ are concyclic for $i=1,\ldots ,n-1.$ Prove that points $A_n,B_n,B_1,A_1$ are also concyclic.
This is especially obvious when the circumcircles of points $\{A_i\}$ and $\{B_i\}$ are concyclic. In this case, the quadrilaterals $A_iB_iB_{i+1}A_{i+1}$ are isosceles trapezoids, and, for even $n,$ so is $A_nB_nB_1A_1.$
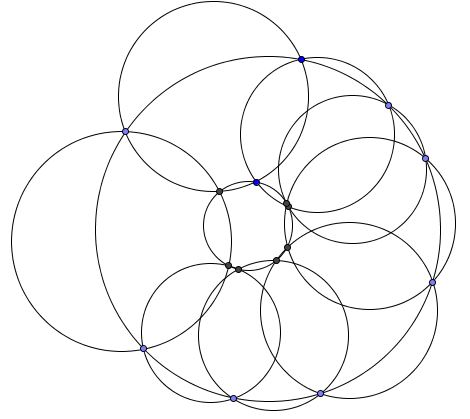
Since every pair of non-intersecting circles could be inverted into concyclic ones, the statement is validated for any two non-intersecting circles.
Inversion - Introduction
- Angle Preservation Property
- Apollonian Circles Theorem
- Archimedes' Twin Circles and a Brother
- Bisectal Circle
- Chain of Inscribed Circles
- Circle Inscribed in a Circular Segment
- Circle Inversion: Reflection in a Circle
- Circle Inversion Tool
- Feuerbach's Theorem: a Proof
- Four Touching Circles
- Hart's Inversor
- Inversion in the Incircle
- Inversion with a Negative Power
- Miquel's Theorem for Circles
- Peaucellier Linkage
- Polar Circle
- Poles and Polars
- Ptolemy by Inversion
- Radical Axis of Circles Inscribed in a Circular Segment
- Steiner's porism
- Stereographic Projection and Inversion
- Tangent Circles and an Isosceles Triangle
- Tangent Circles and an Isosceles Triangle II
- Three Tangents, Three Secants
- Viviani by Inversion
- Simultaneous Diameters in Concurrent Circles
- An Euclidean Construction with Inversion
- Construction and Properties of Mixtilinear Incircles
- Two Quadruplets of Concyclic Points
- Seven and the Eighth Circle Theorem
- Invert Two Circles Into Equal Ones
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73578913
