Apollonian Circles Theorem

Given two points A and B and a number r. What is the locus of points P such that AP/BP = r? The answer is a circle. The circle which is known as the Apollonian Circle. For every positive r there is a different one.

This problem has been treated elsewhere. Here we present a different solution based on the inversion transform. Along the way we show that the whole family of Apollonian circles can be inverted into a family of concentric circles.

Solution

|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|

Copyright © 1996-2012 Alexander Bogomolny

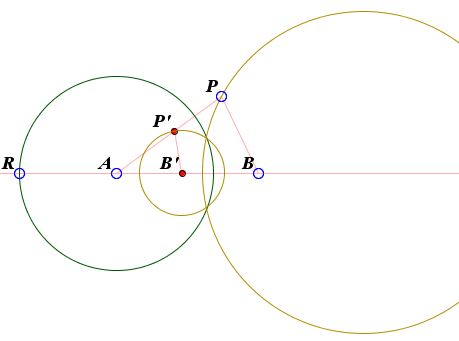
Consider a circle of radius R centered at A. The calculations are simplified by taking R = 1, but, in principle, any circle with center at A will do. So, assume R = 1. Let t be the inversion in this circle. Set t(B) = B' and t(P) = P'.

This means, in particular, that

Triangles AB'P' and APB, in which the sides satisfy (1), also share the angle at A. They are, therefore, similar. It then follows that

From here,

Combining (1) and (3) gives

This tells us that P' lies on a circle of radius 1/rAB centered at B'. In other words, the inversive image of the locus of points P is a circle centered at B'. To repeat, the Apollonian circle defined by the point circles A and B and r > 0 is mapped by t to a circle centered at t(B). This is true for any Apollonian circle defined by A and B, so that the whole family of them is mapped on the family of concentric circles with center t(B).

In establishing Steiner's Porism we showed that any two non-intersecting circles can be inverted into a pair of concentric circles. The above strengthens this assertion with a more direct proof.

The Apollonian circles defined by two point circles are said to be coaxal. This is one of the three varieties of coaxal families.

References

1. D. A. Brannan et al, Geometry, Cambridge University Press, 2002

Inversion - Introduction

• Angle Preservation Property
• Apollonian Circles Theorem
• Archimedes' Twin Circles and a Brother
• Bisectal Circle
• Chain of Inscribed Circles
• Circle Inscribed in a Circular Segment
• Circle Inversion: Reflection in a Circle
• Circle Inversion Tool
• Feuerbach's Theorem: a Proof
• Four Touching Circles
• Hart's Inversor
• Inversion in the Incircle
• Inversion with a Negative Power
• Miquel's Theorem for Circles
• Peaucellier Linkage
• Polar Circle
• Poles and Polars
• Ptolemy by Inversion
• Radical Axis of Circles Inscribed in a Circular Segment
• Steiner's porism
• Stereographic Projection and Inversion
• Tangent Circles and an Isosceles Triangle
• Tangent Circles and an Isosceles Triangle II
• Three Tangents, Three Secants
• Viviani by Inversion
• Simultaneous Diameters in Concurrent Circles

|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|

Copyright © 1996-2012 Alexander Bogomolny