| Manifesto | Bookstore | Contents | Amazon store | Term index | What changed? | Contact | Recommend |
Four Touching Circles: What Is this About?
|
| Buy this applet What if applet does not run? |
(The circled points are draggable.)
Copyright © 1996-2009 Alexander Bogomolny
Four Touching Circles
The applet suggests the following theorem:
| (A) | Let there be 4 circles S1, S2, S3, and S4 each tangent cyclically to its neighbors, so that S1 touches S2 and S4, S2 also touches S3, and the latter touches S4. Prove that the four tangency points are concyclic, i.e. lie on a circle. |
Check the "Inverted diagram" box. You'll see two parallel lines, two tangent circles, each of which is tangent to one of the parallel lines and a line that goes through the three points of tangency. What is this about?
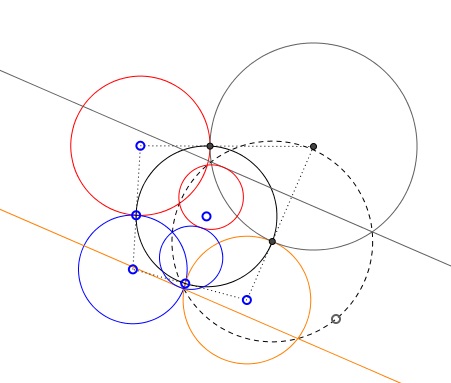
Assume we indeed have a chain of four circles, each touching two of its neighbors. Make an inversion with one point of tangency as the center. Two circles tangent at that point will map on two parallel lines. The other two circles map onto tangent circles each touching one of the parallel lines. (Because of the angle preservation property tangent curves are mapped onto tangent curves.) Observe that
Two parallel lines are homothetic with any point in the plane (but not on the lines) as a legitimate center of homothety.
Two tangent circles are homothetic with the common point of tangency as the center.
This means that that the whole (inverted) configuration is homothetic with the center of homothety at the point of tangency of the two (inverted) circles. Necessarily the points of tangency of the circles with the parallel lines are images of each other under that homothety, such that the three points of tangency are collinear. By the inversion at hand, the line those points are on, is mapped onto a circle passing through the center of inversion.
The proof may now proceed as follows. We used 1 of the points of tangency of the circles S1, S2, S3, and S4 as the center of inversion. The other three points are of course concyclic. Let them lie on circle S. Under the inversion, the images of the three points are collinear. Therefore that circle S passes through the center of inversion - the fourth point of tangency.
Remark
Years after this page was written it came to my attention that the theorem as it was stated above is in fact incorrect. A modification is not difficult and is easily verifiable. The simplest variant is the one proven: if all four tangencies are external the proof goes through without a modifications. It remains also valid if the number of external tangencies is even: 0, 2, or 4. The proof fails and the theorem no longer holds if the number of external tangencies is odd: 1 or 3.
I do not remember my original source for the problem. However, it appears in the second volume (in Russian) of I. M. Yaglom's Geometric Transformations (Problem 216) in a wrong formulation and also in volume 2 of V. V. Prasolov's Problems in Planimetry (Problem 28.5) in a limited formulation (all tangencies are required to be external.)
Observe that the inverted diagram lets you modify the circle configuration. However all possible modifications will result in an even number of external tangencies.
While trying to ascertain the properties of the four circle configuration I wrote another applet with an elementary but an incomplete proof of the theorem. The applet allows for a more direct handling of the configuration without invoking the inversion.
The third applet is the most general and offers a direct observation of the phenomenon: in case of the odd number of external tangencies the four contact points cease to be concyclic.
Inversion - Introduction
- Angle Preservation Property
- Apollonian Circles Theorem
- Archimedes' Twin Circles and a Brother
- Bisectal Circle
- Chain of Inscribed Circles
- Circle Inscribed in a Circular Segment
- Circle Inversion: Reflection in a Circle
- Circle Inversion Tool
- Feuerbach's Theorem: a Proof
- Four Touching Circles
- Hart's Inversor
- Inversion in the Incircle
- Inversion with a Negative Power
- Miquel's Theorem for Circles
- Peaucellier Linkage
- Polar Circle
- Poles and Polars
- Radical Axis of Circles Inscribed in a Circular Segment
- Steiner's porism
- Stereographic Projection and Inversion
- Tangent Circles and an Isosceles Triangle
- Tangent Circles and an Isosceles Triangle II
- Three Tangents, Three Secants
Copyright © 1996-2009 Alexander Bogomolny
| 34220030 |  |
