Inversion with Negative Power: What is this about?
A Mathematical Droodle
| What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander BogomolnyInversion with Negative Power
| What if applet does not run? |
The applet is supposed to remind of the symmetry in circle - inversion. The inverse image A' of a point A has the property that all circles perpendicular to the circle of inversion t and passing through A invariably pass through A'.
The current situation is slightly different:
| All circles through two diametrically opposite points on a given circle t and point A not at the center of t also pass through another point A'. |
(In the applet the circle t is defined by its draggable center O and point R.)
Proof
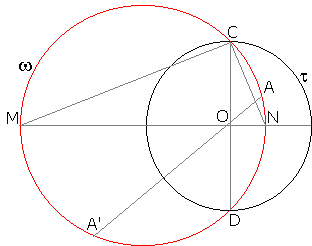
|
Let CD be a diameter of t, w the circle through C, D and A, and let MN is the diameter of w that passes through O. CD is then perpendicular to MN.
ΔMCN is right, therefore
| (1) | MO×NO = CO2 = OR2. |
Let A' be the second point of intersection of OA with w. By the Intersecting Chords Theorem,
| (2) | MO×NO = OA×OA'. |
Combining (1) and (2) gives
| (3) | OA×OA' = OR2, |
which appears exactly like the inversion identity, but is not quite the same. The difference is in that formerly the points A and A' lay on the same side from O, while now O separates the two. If we consider OA and OA' as signed segments, then (3) should be corrected to
| (4) | OA×OA' = -OR2. |
The latter defines inversion with a negative power. The applet demonstrates the geometric meaning of such a transformation. Inversion in t with the power
Inversion - Introduction
- Angle Preservation Property
- Apollonian Circles Theorem
- Archimedes' Twin Circles and a Brother
- Bisectal Circle
- Chain of Inscribed Circles
- Circle Inscribed in a Circular Segment
- Circle Inversion: Reflection in a Circle
- Circle Inversion Tool
- Feuerbach's Theorem: a Proof
- Four Touching Circles
- Hart's Inversor
- Inversion in the Incircle
- Inversion with a Negative Power
- Miquel's Theorem for Circles
- Peaucellier Linkage
- Polar Circle
- Poles and Polars
- Ptolemy by Inversion
- Radical Axis of Circles Inscribed in a Circular Segment
- Steiner's porism
- Stereographic Projection and Inversion
- Tangent Circles and an Isosceles Triangle
- Tangent Circles and an Isosceles Triangle II
- Three Tangents, Three Secants
- Viviani by Inversion
- Simultaneous Diameters in Concurrent Circles
- An Euclidean Construction with Inversion
- Construction and Properties of Mixtilinear Incircles
- Two Quadruplets of Concyclic Points
- Seven and the Eighth Circle Theorem
- Invert Two Circles Into Equal Ones
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73578716
