Symmetries in a Triangle
The following problem by Paul Yiu has been published in Crux Mathematicorum:
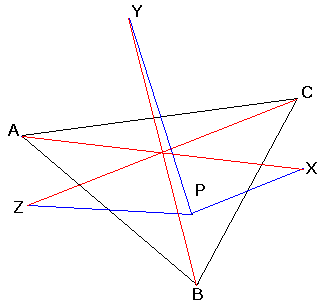
If ABC is a triangle and P any point in the plane distinct from A, B, C and if X, Y, Z are the symmetries of P with respect to the midpoints of BC, CA, AB respectively, show that AX, BY, CZ concur.
|Contact| |Front page| |Contents| |Geometry| |Up|
Solution

If ABC is a triangle and P any point in the plane distinct from A, B, C and if X, Y, Z are the symmetries of P with respect to the midpoints of BC, CA, AB respectively, show that AX, BY, CZ concur.
The solution is by Michael Lambrou posted at the Hyacinthos forum.
(I purposely do not draw the triangle ABC).

If you imagine you are looking at the figure from a three dimensional perspective, so to speak from above, you can see a parallelepiped. Then Paul's problem to show that the lines AX, BY, CZ concur amounts to saying that these lines are the diagonals of the figure.
The same could be said a little differently. Consider a point P' in 3D such that PP' is perpendicular to the plane of ΔABC. Let points X', Y', and Z' be symmetries of P' in the midpoints of CB, BA, and AC, respectively. Then points A, B, C, P', X', Y', Z' serve as vertices of a parallelepiped. The required concurrence of AX', BY' and CZ' is obvious. Now observe that the original configuration is the orthogonal projection of that parallelepiped onto the plane. The conclusion follows since projection preserves concurrence.
Note that our approach makes it also obvious that triangle ABC and XYZ are in fact equal.
(This page has been expanded elsewhere with two additional proofs.)
There are further examples where stepping out of a 2 dimensional plane into 3 dimensions makes a problem at hand easily solvable:
2D Problems That Benefit from a 3D Outlook
- Four Travellers, Solution
- Desargues' Theorem
- Soddy Circles and Eppstein's Points
- Symmetries in a Triangle
- Three Circles and Common Chords
- Three Circles and Common Tangents
- Three Equal Circles
- Menelaus from 3D
- Stereographic Projection and Inversion
- Stereographic Projection and Radical Axes
- Sum of Squares in Equilateral Triangle
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny
73581502
