Tangent Circles and an Isosceles Triangle
Solution by N. Bowler

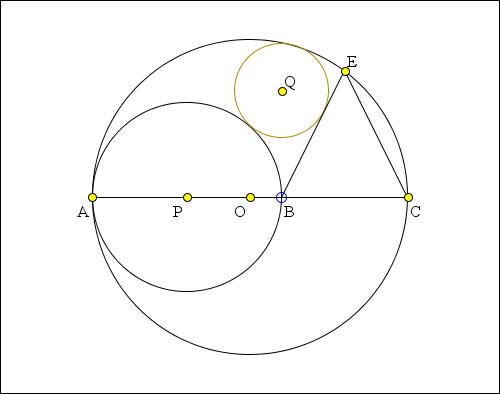
The applet presents a solution to the following Sangaku problem: Given a circle S with center O and diameter AC and point B on AC. Form circle G with center P and diameter AB and an isosceles triangle BCE with E on the circle S. Circle W with center Q is inscribed in the curvilinear triangle formed by circles S and G and the line BE. Prove that QB is perpendicular to AC.

What if applet does not run? -->

I shall use inversion. I shall denote the inverse of any object by the name of that object followed by a '.

First note that the problem is equivalent to showing that the circle with centre on the perpendicular from B, and tangent to BE and to G is also tangent to S. I shall still call this circle W.

Invert with respect to B, i.e., in a circle centered at B and some radius r, say.

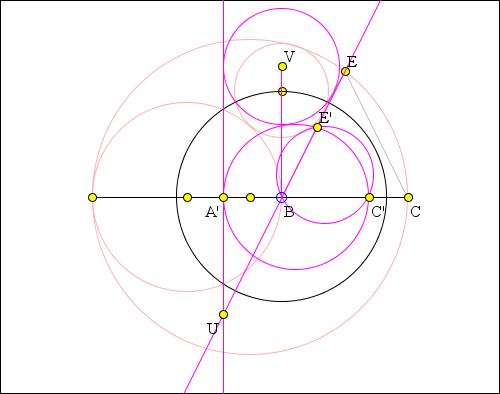
1. Step 1: C'BE' will be similar to EBC and so isosceles. This is because BC·BC' = r² = BE·BE', such that BC/BE = BE'/BC'. It follows that also BC'/C'E' = CE/BE, but in DBCE we have CE = BE.

2. Step 2: S' will be the circle on A'C' as diameter, and G' the tangent to it at A'.

3. Step 3: Let U be the intersection of G' with E'B. Then A'UE' = pi/2 - UBA' = pi/2 - E'BC' = pi/2 - C'E'B = UE'A' so A'UE' is isosceles.

4. Step 4: Let V be the centre of W'. Since W' is tangent to both G' and BE', V lies on the bisector of A'UB. So VUB = A'UV = BVU and so also BVU is isosceles.

5. Step 5: Let L be the centre of S', and call the radius of this circle R. Call the radius of W' r.

   There are right angles everywhere, so we may now indulge ourselves with a Pythagorean orgy:

   LV2 = LB2 + BV2   = (R - A'B)2 + BU2   = (R-r)2 + A'B2 + A'U2   = (R-r)2 + r2 + A'E'2   = (R-r)2 + r2 + A'C'2 - E'C'2   = (R-r)2 + r2 + 4R2 - BC'2   = (R-r)2 + r2 + 4R2 - (2R-r)2   = R2 + 2Rr + r2   = (R + r)2.

   So that W' is tangent to S' and so W is tangent to S as required.

Another solution makes use of inversion with negative power.

Inversion - Introduction

• Angle Preservation Property
• Apollonian Circles Theorem
• Archimedes' Twin Circles and a Brother
• Bisectal Circle
• Chain of Inscribed Circles
• Circle Inscribed in a Circular Segment
• Circle Inversion: Reflection in a Circle
• Circle Inversion Tool
• Feuerbach's Theorem: a Proof
• Four Touching Circles
• Hart's Inversor
• Inversion in the Incircle
• Inversion with a Negative Power
• Miquel's Theorem for Circles
• Peaucellier Linkage
• Polar Circle
• Poles and Polars
• Ptolemy by Inversion
• Radical Axis of Circles Inscribed in a Circular Segment
• Steiner's porism
• Stereographic Projection and Inversion
• Tangent Circles and an Isosceles Triangle
• Tangent Circles and an Isosceles Triangle II
• Three Tangents, Three Secants
• Viviani by Inversion
• Simultaneous Diameters in Concurrent Circles
• An Euclidean Construction with Inversion
• Construction and Properties of Mixtilinear Incircles
• Two Quadruplets of Concyclic Points
• Seven and the Eighth Circle Theorem
• Invert Two Circles Into Equal Ones

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny