Three equal circles Here is the problem: If three circles having the same radius pass through a point, the circle through their other three points of intersection also has the same radius. The circles are denoted k, l, m. The points of their intersection are 0, A, B, C. Solution                                           Solution The picture above is somewhat incomplete. We are dealing with circles after all. A circle is defined by its center and its radius. In the original picture the center points are missing. Let denote them K,L,M. Now it also might be important to indicate what distances are equal. For this is our data: the three circles all have the same radius. 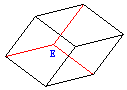The nine equal segments appear to form a well known shape. It's a projection of a parallelepiped on a plane. Normally we would draw such a projection with three more edges that were hidden above. Now we have 12 equal segments. The newly drawn edges meet at a previously hidden vertex E which is equidistant from points A, B, and C. (There is a very interesting circumstance where the above configuration emerges naturally but still unexpectedly.) References R. Honsberger, Mathematical Gems II, MAA, 1976, pp. 20-21 G. Polya, Mathematical Discovery, John Wiley and Sons, 1981, Ch. 10. 2D problems that benefit from a 3D outlook 4 Travellers Desargues' Theorem Soddy Circles and Eppstein's Points Symmetries in a Triangle Three Circles and Common Chords Three Circles and Common Tangents Three Equal Circles Copyright © 1996-2008 Alexander Bogomolny

28675321

Search:

All Products Apparel Baby Beauty Books DVD Electronics Home & Garden Gourmet Food Personal Care Jewelry & Watches Housewares Magazines Musical Instruments Music Computers Camera & Photo Software Sports & Outdoors Tools & Hardware Toys & Games VHS Computer Games Cell Phones

Keywords:

Latest on CTK Exchange Math Posted by Laura 2 messages 06:56 AM, Apr-15-08 Divisibility rules - Jargon buste ... Posted by Carolyn 2 messages 08:35 AM, Apr-04-08 product of fractions Posted by ke_45 3 messages 08:37 AM, May-06-08 Distance to the horizon Posted by Monty 3 messages 04:38 PM, May-08-08 Mistake on the page (an aside, Be ... Posted by Max 4 messages 10:28 AM, Feb-28-08 Nim Games - a query Posted by Akash Kumar 1 messages 08:53 AM, Apr-15-08 A typo in Posted by alexwajn 1 messages 11:36 PM, Apr-19-08