Invert Two Circles Into Equal Ones

What is this about?

Problem

Assume that inversion in circle $c$ maps circle $c_1$ onto circle $c_2.$ Then, for any point $X\in c,$ any inversion with center $X$ maps $c_1$ and $c_2$ into equal circles.

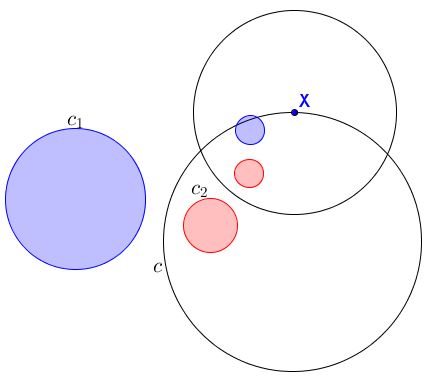
Seven and the Eighth Circle Theorem - lemma

Solution

A circle through the center of inversion maps onto a straight line. Thus circle $c$ becomes a straight line under inversion with center $X.$ Circles $c_1$ and $c_2$ are mapped into each other's reflections in this line, which are therefore equal.

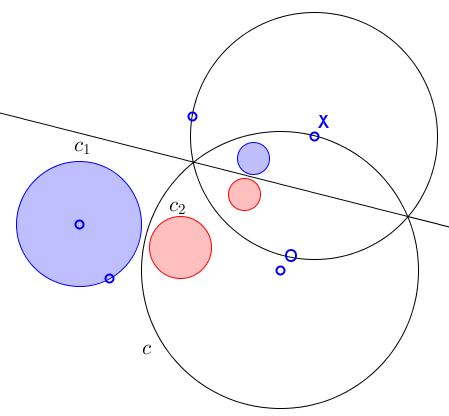
Seven and the Eighth Circle Theorem - solution

Corollary

Any two circles of which neither is entirely within the other can be mapped into equal ones by two successive inversions.

The first inversion needs to map the given circles into each other. Next, we apply the already proved statement by choosing an arbitrary point on the circle of inversion as the center of the second transform.

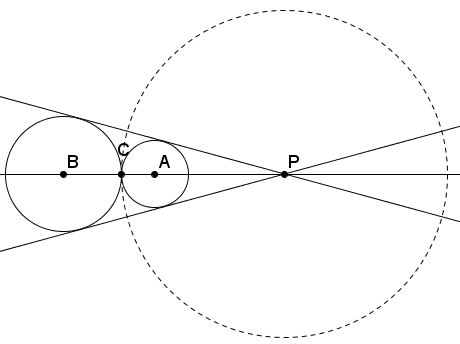
Seven and the Eighth Circle Theorem - corollary

The diagram above shows how to choose the circle of inversion for the first step when the two circles are tangent to each other. When they cross, the situation is analogous.

When the given circles do not have common points, consider the diagram below:

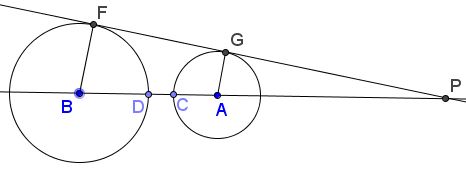
Seven and the Eighth Circle Theorem - corollary, third case

Let $R=BF$ and $r=AE.$ From the similarity of triangles $BFP$ and $AEP,$ $\displaystyle\frac{BP}{R}=\frac{AP}{r}=t,$ so that $BP=Rt$ and $AP=rt,$ for some positive $r.$ An inversion that maps circle $B(D)$ onto circle $A(C)$ maps $D$ onto $C.$ By definition, its radius $\rho$ should satisfy $\rho^{2}=CP\cdot DP=(t^{2}-1)Rr.$ It is easy to see that so defined radius determines the required inversion.

Acknowledgment

This is problem 3.8.15 from H. Eves, A Survey of Geometry.

Inversion - Introduction

71931752