A Restored Sangaku Problem

The sangaku discussed below was originally hung [Fukagawa and Rothman, pp. 194-195] in 1806 in the Atsuta shrine by Ehara Masanori, a disciple of Kusaka Makoto (1764-1839). The tablet, which contained only this problem and no solution, was subsequently lost. However, at an unknown date the mathematician Kitagawa Moko (1763-1839) visited the shrine and recorded the sangaku in his note "Kyuka Sankei," or "Nine Flowers Mathematics," along with his solution. More recently the shrine constructed a replica from Kitagawa's manuscript. Fukagawa and Rothman reproduce Kitagawa's solution with a warning: This may be the most involved exploitation of the Pythagorean theorem you have ever seen.

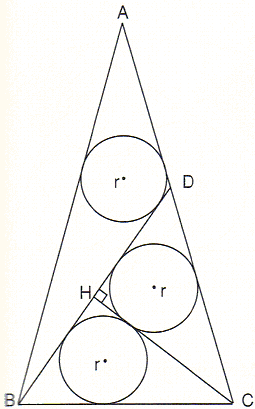
The problem is this: ΔABC is isosceles. Two lines BD and CH divide it into three smaller triangles, each of which circumscribes a circle of the same radius r. Find r in terms of CH.

Following [Fukagawa and Rothman, pp. 212-216], I shall give Kitagawa's solution and then, on a separate page, a solution by J. M. Unger.

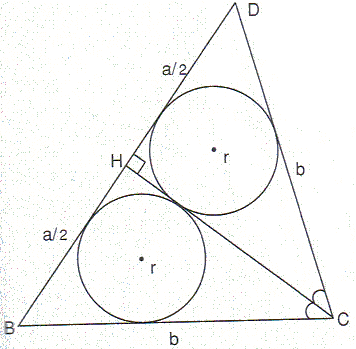
First, notice from the figure above that triangle CDB is isosceles. Therefore let b = BC = CD, as indicated. We also let a = BD and k = CH. Next, as shown below, mark with a compass two points D' on AB and D'' on AC such that BD = BD' = CD'' = a. Because ΔABC is isosceles, D'T' = D''T'' and by construction D'T' = DT; consequently DT = D''T''.

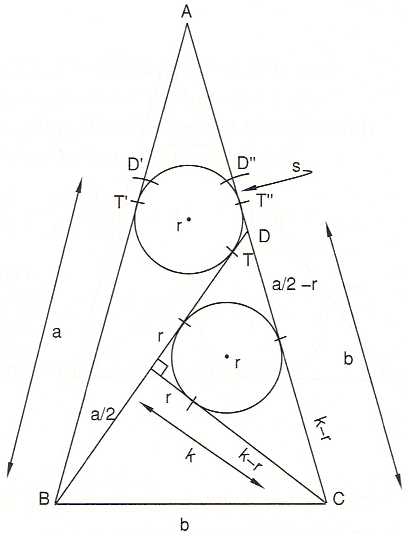
T and T'' are equidistant from D and therefore DT'' = D''T''. Defining s = DT = DT'' we can write

Further, by examining the tangents in the figure above, we see that

Hence, from equation (1)

Also, with the Pythagorean theorem, from either ΔBCH or ΔCDH, b² = (a/2)² + k². Squaring equation (2) and equating the two expressions quickly yields

Next, as shown below, inscribe a circle of radius R in triangle BCD.

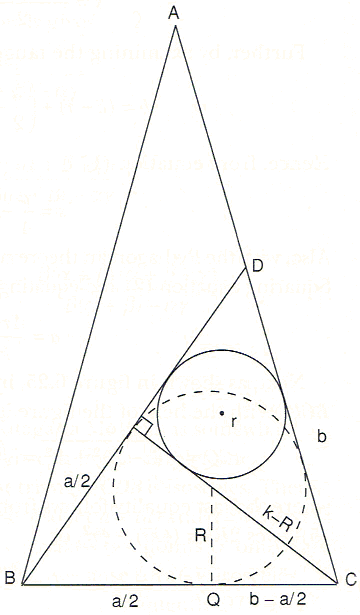
With the help of the figure it is easy to show that

where the last equality follows from equation (2). Squaring equation (5) gives 2Rk = (4kr) - 4r², or

The strategy is now to eliminate R in favor of r and k. Applying the Pythagorean theorem directly to the figure below gives

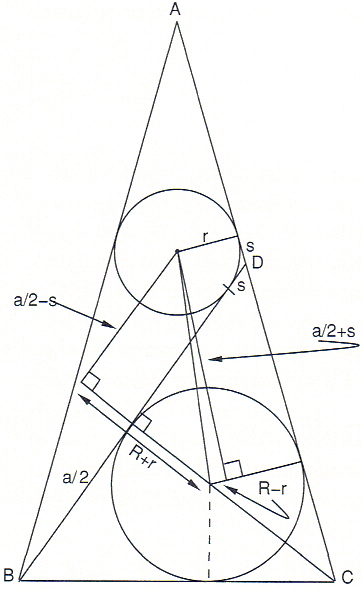
or, after simplifying,

The problem is almost solved. We now replace R on the left of equation (7) by equation (6) and as on the right by the expressions in equations (3) and (4) to get

which gives the cubic

From any of the figures, the relevant root is k = 4r, and thus we have the final result

References

1. H. Fukagawa, A. Rothman, Sacred Mathematics: Japanese Temple Geometry, Princeton University Press, 2008

Sangaku

1. Sangaku: Reflections on the Phenomenon
2. Critique of My View and a Response
3. 1 + 27 = 12 + 16 Sangaku
4. 3-4-5 Triangle by a Kid
5. 7 = 2 + 5 Sangaku
6. A 49^th Degree Challenge
7. A Geometric Mean Sangaku
8. A Hard but Important Sangaku
9. A Restored Sangaku Problem
   • A better solution to a difficult sangaku problem
10. A Sangaku: Two Unrelated Circles
11. A Sangaku by a Teen
12. A Sangaku Follow-Up on an Archimedes' Lemma
13. A Sangaku with an Egyptian Attachment
14. A Sangaku with Many Circles and Some
15. A Sushi Morsel
16. An Old Japanese Theorem
17. Archimedes Twins in the Edo Period
18. Arithmetic Mean Sangaku
19. Bottema Shatters Japan's Seclusion
20. Circles and Semicircles in Rectangle
21. Circles in a Circular Segment
22. Circles Lined on the Legs of a Right Triangle
23. Equal Incircles Theorem
24. Equilateral Triangle, Straight Line and Tangent Circles
25. Equilateral Triangles and Incircles in a Square
26. Five Incircles in a Square
27. Four Hinged Squares
28. Four Incircles in Equilateral Triangle
29. Gion Shrine Problem
30. Harmonic Mean Sangaku
31. Heron's Problem
32. In the Wasan Spirit
33. Incenters in Cyclic Quadrilateral
34. Japanese Art and Mathematics
35. Malfatti's Problem
36. Maximal Properties of the Pythagorean Relation
37. Neuberg Sangaku
38. Out of Pentagon Sangaku
39. Peacock Tail Sangaku
40. Pentagon Proportions Sangaku
41. Pythagoras and Vecten Break Japan's Isolation
42. Radius of a Circle by Paper Folding
43. Review of Sacred Mathematics
44. Sangaku à la V. Thebault
45. Sangaku and The Egyptian Triangle
46. Sangaku in a Square
47. Sangaku Iterations, Is it Wasan?
48. Sangaku with 8 Circles
49. Sangaku with Three Mixtilinear Circles
50. Sangaku with Versines
51. Sangakus with a Mixtilinear Circle
52. Sequences of Touching Circles
53. Square and Circle in a Gothic Cupola
54. Tangent Circles and an Isosceles Triangle
55. The Squinting Eyes Theorem
56. Steiner's Sangaku
57. Three Incircles In a Right Triangle
58. Three Squares and Two Ellipses
59. Three Tangent Circles Sangaku
60. Triangles, Squares and Areas from Temple Geometry
61. Two Arbelos, Two Chains
62. Two Circles in an Angle
63. Two Sangaku with Equal Incircles

Copyright © 1996-2009 Alexander Bogomolny