Five Incircles in a Square: What Is This About?
A Mathematical Droodle

Explanation

Copyright © 1996-2010 Alexander Bogomolny

Here we have a very characteristic sangaku - a Temple geometry - problem. Most of geometric sangaku dealt with several circles inscribed in other circles or other shapes. In addition, most often a sangaku was a computational problem as opposed to problems that require a proof. The problem below is a little of both: a proof of the result is supported by a chain of calculations.

In the manner of proof #3 of the Pythagorean theorem, four equal right triangles and a small square are combined into a larger square. Circles are inscribed into the four triangles and the inner square. A question: What can be said of the configuration where all five circles have equal radii?

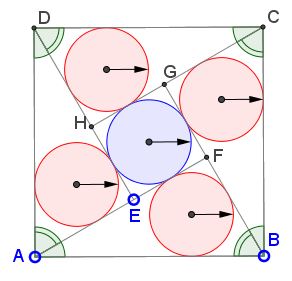
So assume the triangles have legs a and b (a > b) and hypotenuse c. Then, as we know, the inradius for the triangle is given by

On the other hand, the radius of the circle inscribed into the inner square is obviously

Equating the two we get

which means that the angle opposite b is 30° and the other one is 60°. From here we easily find the common inradius: r = c·(√3 - 1)/4.

Most of the sangaku problems are much more difficult.

References

1. H. Fukagawa, D. Pedoe, Japanese Temple Geometry Problems, The Charles Babbage Research Center, Winnipeg, 1989

   Write to:

   Charles Babbage Research Center
   P.O. Box 272, St. Norbert Postal Station
   Winnipeg, MB
   Canada R3V 1L6

Sangaku

1. Sangaku: Reflections on the Phenomenon
2. Critique of My View and a Response
3. 1 + 27 = 12 + 16 Sangaku
4. 3-4-5 Triangle by a Kid
5. 7 = 2 + 5 Sangaku
6. A 49^th Degree Challenge
7. A Geometric Mean Sangaku
8. A Hard but Important Sangaku
9. A Restored Sangaku Problem
   • A better solution to a difficult sangaku problem
   • A Trigonometric Solution to a Difficult Sangaku Problem
10. A Sangaku: Two Unrelated Circles
11. A Sangaku by a Teen
12. A Sangaku Follow-Up on an Archimedes' Lemma
13. A Sangaku with an Egyptian Attachment
14. A Sangaku with Many Circles and Some
15. A Sushi Morsel
16. An Old Japanese Theorem
17. Archimedes Twins in the Edo Period
18. Arithmetic Mean Sangaku
19. Bottema Shatters Japan's Seclusion
20. Circles and Semicircles in Rectangle
21. Circles in a Circular Segment
22. Circles Lined on the Legs of a Right Triangle
23. Equal Incircles Theorem
24. Equilateral Triangle, Straight Line and Tangent Circles
25. Equilateral Triangles and Incircles in a Square
26. Five Incircles in a Square
27. Four Hinged Squares
28. Four Incircles in Equilateral Triangle
29. Gion Shrine Problem
30. Harmonic Mean Sangaku
31. Heron's Problem
32. In the Wasan Spirit
33. Incenters in Cyclic Quadrilateral
34. Japanese Art and Mathematics
35. Malfatti's Problem
36. Maximal Properties of the Pythagorean Relation
37. Neuberg Sangaku
38. Out of Pentagon Sangaku
39. Peacock Tail Sangaku
40. Pentagon Proportions Sangaku
41. Pythagoras and Vecten Break Japan's Isolation
42. Radius of a Circle by Paper Folding
43. Review of Sacred Mathematics
44. Sangaku à la V. Thebault
45. Sangaku and The Egyptian Triangle
46. Sangaku in a Square
47. Sangaku Iterations, Is it Wasan?
48. Sangaku with 8 Circles
49. Sangaku with Quadratic Optimization
50. Sangaku with Three Mixtilinear Circles
51. Sangaku with Versines
52. Sangakus with a Mixtilinear Circle
53. Sequences of Touching Circles
54. Square and Circle in a Gothic Cupola
55. Tangent Circles and an Isosceles Triangle
56. The Squinting Eyes Theorem
57. Steiner's Sangaku
58. Three Incircles In a Right Triangle
59. Three Squares and Two Ellipses
60. Three Tangent Circles Sangaku
61. Triangles, Squares and Areas from Temple Geometry
62. Two Arbelos, Two Chains
63. Two Circles in an Angle
64. Two Sangaku with Equal Incircles

Copyright © 1996-2010 Alexander Bogomolny