Three Incircles in a Triangle:
What Is This About?
A Mathematical Droodle

---

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at https://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

---

What if applet does not run?

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

This is an extension of another result concerning three incircles in a triangle.

Theorem

Let the incircle of ΔABC touch the side BC at point T. Let X be another point on BC. Consider incircles of triangles ABX and ACX. Then the internal common tangent of the two circles other than AX, passes through T. Additionally, both X and T lie on a circle constructed on the segment joining the incenters of triangle ABX and ACX as diameter.

(For a partial history of the problem, a context and the credits, refer to D. Grinberg's post (Theorems 1 and 2) at the CTK Exchange.)

Proof

Below, I shall refer to the following configuration, where X lies to the right of T.

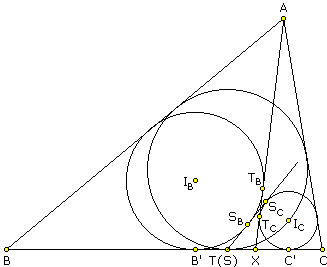
Let I_B and I_C be the incenters of triangles ABX and ACX, respectively; T_B and T_C are the points where their incircles touch AX. AX is thus an internal common tangent of the two circles. Assume their other internal common tangent S_BS_C crosses BC in point S. We want to show that S = T.

Obviously,

(1)

T_BT_C = S_BS_C.

If B' and C' are the points where the two incircles touch BC, then SB' = SS_B and SC' = SS_C, so that

(2)

S_BS_C = SS_C - SS_B = SC' - SB'.

On the other hand,

(3)

S_BS_C = T_BT_C = XT_B - XT_C = XB' - XC',

wherefrom

(4)

SB' + XB' = SC' + XC'.

And we conclude that the midpoints of segments SX and B'C' coincide, and therefore SB' = XC'. Now, as was shown by V. Zajic,

(5)

TX = T_BT_C.

From (3) and (5) we also have

(6)

TX + XC' = XB' = TB' + TX,

which implies XC' = TB', so that, finally, TB' = SB' and T = S.

Let's now consider the circle, say g, with diameter I_BI_C. I_B lies on the bisector of angle BXA, while I_C lies on the bisector of the supplementary angle CXA. Since the two bisectors are orthogonal, X lies on g. Since TS_BS_C is also tangent to the two circles, I_B and I_C lie on the bisectors of BTS_BS_C and CTS_BS_C - another pair of supplementary angles. The two are again orthogonal, and therefore T, too, lies on g.

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny