Cut The Knot!

An interactive column using Java applets
by Alex Bogomolny

Bride's Chair

August 2003

Given its unmatched importance in mathematics and applications, it is wonderful that the Pythagorean theorem (Elements I.47) is apparently not as widely known as one could expect:

In right-angled triangles the square on the side subtending the right angle is equal to the squares on the sides containing the right angle.

The pictorial representation of the theorem is known in mathematical folklore under many names, the bride's chair, being probably the most popular, but also as the Franciscan's cowl, the peacock's tail and the windmill. In Russia the common name, I believe, is rather pragmatic: Pythagorean pants. According to D. E. Smith [Smith, p. 289], the Arabs call it the Figure of the Bride. He also mentions [Smith, p. 290], with a reference to E. Lucas' Récréations Mathématiques, that the Greeks call it the theorem of the married women, while Bhãskara is said to have spoken of it as the chase of the little married women.

(Florian Cajori ascribes (Am Math Monthly, f 6, no 3, 1899, p. 72) the source of the Bride's Chair designation to a mistranslation of the Greek word numfh "applied to the theorem by a Byzantine writer of the 13th century. This Greek word admits of two meanings, 'bride' and 'winged insect.' The figure of the right triangle with the three squares suggests an insect but Behâ Eddîn apparently translated the word as 'bride'." Probably out of respect of the famous mathematician and his theorem.)

In a book of philosophical (!) notes and essays, R. Smullyan tells (pp. 21-22) of an episode in his teaching career. After drawing the diagram, he requested the class to choose the larger of the sum of the small squares and the large square. "Interestingly enough, about half the class opted for the one large square and half for the two small ones. ... Both groups were equally amazed when told that it would make no difference."

Euclid himself generalized the diagram (Elements VI.31) by replacing squares with other shapes. Pappus replaced (Mathematical Collection, Book IV) the squares with arbitrary parallelograms drawn on the sides of an arbitrary triangle.

A different kind of generalization kept the squares on the sides with a relaxed requirement on the angles of the triangle. Euclid himself considered an arbitrary triangle with squares on its sides in Prop. 63 of his surviving work The Data. In the 19th century (1817), Vecten also studied arbitrary triangles with squares on their sides.

We may immediately observe several simple properties of Vecten's configuration. First of all, the "add-on" triangles ABaCa, AbBCb, AcBcC have the same area as ΔABC [Exercices, p. 736, Five Hundred, #295]. To see this, rotate (drag the slider), e.g., ΔABaCa through 90° clockwise till Ba coincides with C. Then CA will serve as a median of ΔBCC'a that splits the triangle into two of equal area. (More recently, the fact was observed by R. Webster.) Also, after the rotation, the median AMa will become a midline in ΔBCC'a, parallel to its side BC, which implies the second property, viz., the same line serves as a median in ΔABaCa and an altitude in ΔABC. It also has been observed that AMa = BC/2 and similarly for the other medians.

The triangles ABaCa, AbBCb, AcBcC are known as flanks of ΔABC. The relationship is symmetric: a triangle is a flank of its own flanks. Thus, for example, we can also claim that the same line serves as an altitude in ΔABaCa and a median in ΔABC. We may restate this as follows.

Let, for a triangle center P of ΔABC, Pa, Pb, and Pc denote its namesakes in triangles ABaCa, AbBCb, AcBcC. Thus, for example, Ga stands for the centroid (the meeting point of the medians) of triangle ABaCa. We then have two facts.

(1)AGa, BGb, and CGc concur in H, and
(2)AHa, BHb, and CHc concur in G,

where G and H are the centroid and the orthocenter of ΔABC.

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at http://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

Following are additional properties of Vecten's configuration, see [Exercices, pp. 860-861]:

  1. Lines AAb and BBa meet on the C-altitude of ΔABC [Exercices, p. 225].

  2. Lines AAb and CCb are perpendicular and equal. (This follows from the congruence of triangles ABAb and CbBC.) Assume AAb and CCb meet at point Sb and introduce similarly Sa and Sc.

  3. Line AcCa passes through Sb and bisects a pair of angles at that point. (Quadrilateral ACaCbSb is cyclic as having opposite angles at Ca and Sb both 90°. In the circumcircle, angles ASbCa and ACbCa, the latter being 45°, are subtended by the same chord ACa. Hence angle ASbCa is also 45°.)

  4. Lines ASa, BSb, and CSc are concurrent and each passes through the center of one of Vecten's squares.

  5. Let Ta, Tb, and Tc denote the centers of Vecten's squares BCAcAb, etc. Then ATa is equal and perpendicular to TbTc.

  6. AcBc2 + BaCa2 + AbCb2 = 3(AB2 + BC2 + AC2) [Exercices, p. 736].

(Several additional properties of the configuration are listed on a separate page.)

Ernst Wilhelm Grebe was the first to call the common point of ATa, BTb, and CTc the Vecten point. There are actually two of them depending on whether the squares have been drawn outwardly (the first Vecten point) or inwardly (the second Vecten point) with regard to ΔABC.

Created with GeoGebra

Further results were obtained by Ernst Wilhelm Grebe in 1847 and expanded by F. van Lamoen in 2001.

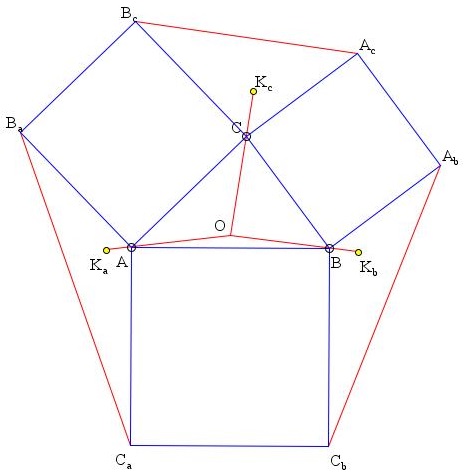
van Lamoen's frienship between the circumcenter and Lemoine's point

Grebe has shown [Exercices, p. 1181] that if the outer sides of Vecten's squares have been extended to form ΔA'B'C', then the latter is similar, in fact homothetic, to ΔABC. The center of homothety is known as Lemoine's point or (in Germany) as Grebe's point. More neutrally, being the point of intersection of the symmedians in ΔABC, it is also called the symmedian point K. For K the distances to the sides of ΔABC are proportional to the sides themselves [Honsberger, p. 59], and this is the reason for the validity of Grebe's theorem.

For the same reason, another triangle, viz., the triangle OaObOc formed by the circumcenters of the flanks is also homothetic to ΔABC at K. The points O and K thus stand in a certain relationship, which F. van Lamoen termed friendship.

In general, centers P and Q are friends if ΔABC is perspective to ΔPaPbPc at Q. Because of the symmetry of the flank relationship, friendship is also symmetric: if ΔABC and ΔPaPbPc are perspective at Q, then ΔABC and ΔQaQbQc are perspective at P.

What has been shown so far is that O and K are friends, as are G and H (1-2). Quite obviously, the incenter I befriends itself. It's not the only point with that property.

O. Bottema has noticed (see a reference in F. van Lamoen's) that the midpoint M of AbBa does not depend on C.

Created with GeoGebra

Created with GeoGebra

Furthermore, he proved that triangles AMB and AcMBc are both right (at M) and isosceles. Point M therefore serves as the center of the square constructed on AB inwardly to ΔABC and of another, constructed on AcBc inwardly to the flank AcBcC. CM is the C-cevian in ΔABC and ΔAcBcC playing the same role in both. We conclude that the second Vecten point that lies at the intersection of such cevians is its own friend.

Similar isosceles triangles on the sides of a given triangle ABC are the subject of Kiepert's theorem that asserts that the outer apexes of the Kiepert triangles form a triangle perspective to ΔABC. The Kiepert triangles are completely defined by the base angle f (mod p) of the isosceles triangles, and the above perspector is known as the Kiepert perspector K(f). Naturally, the second Vecten point is K(-p/4), where the sign minus indicates that the triangles have been constructed inwardly.

F. van Lamoen's proves a more general fact, viz., that the Kiepert perspectors K(f) and K(p/2 - f) are related by friendship. In particular, the Fermat points K(±p/3) are friends with respective Napoleon's points K(±p/6).

Also, since the first Vecten point is none other than K(p/4), it follows that the first, like the second, Vecten point befriends itself as well.

Created with GeoGebra

A fitting redress for the old diagram.

(Further results could be found in the already quoted paper by F. van Lamoen and at this site .)

References

  1. E. J. Barbeau, M. S. Klamkin, W. O. J. Moser, Five Hundred Mathematical Challenges, MAA, 1995.
  2. C. M. Taisbak, Euclid's Data: The Importance of Being Given, Museum Tusculanum (June 2003).
  3. F. G.-M., Exercices de Géométrie, Éditions Jacques Gabay, sixiéme édition, 1991
  4. R. Honsberger, Episodes in Nineteenth and Twentieth Century Euclidean Geometry, MAA, 1995.
  5. C. Pritchard, General Introduction, in The Changing Shape of Geometry, edited by C. Pritchard, Cambridge University Press, 2003
  6. D. E. Smith, History of Mathematics, v. II, Dover, 1958
  7. R. Smullyan, 5000 B.C. and Other Philosophical Fantasies, St. Martin's Press, 1983
  8. F. van Lamoen, Friendship Among Triangle Centers, Forum Geometricorum 1 (2001), pp. 1-6.
  9. R. Webster, Bride's Chair Revisited, Mathematical Gazette 78 (November 1994), pp. 345-346. (Reprinted in Pritchard, pp. 246-247.)
  10. I. Warburton, Bride's Chair Revisited Again!, Mathematical Gazette 80 (November 1996), pp. 557-558. (Reprinted in Pritchard, pp. 248-250.)

Related material
Read more...

  • Bride's Chair: an Interactive Gizmo
  • Desargues in the Bride's Chair(with Pythagoras)
  • Joseph Keech in Bride's Chair
  • Concyclic Points in Bride's Chair
  • A Square in the Chair

    • |Contact| |Front page| |Contents| |Geometry| |CTK|

    Copyright © 1996-2018 Alexander Bogomolny

    71752590