Geometric Meaning of the Geometric Mean
The geometric mean of two positive numbers $a\;$ and $b\;$ is the (positive) number g whose square equals the product $ab\;$:
$g^{2} = ab\;$.
While it is possible to (at least partially) adapt the definition to handle negative numbers, I do not believe this is ever done.
The geometric mean then answers this question: given a rectangle with sides $a\;$ and $b\;$, find the side of the square whose area equals that of the rectangle. In all likelihood, this particular problem gave that number its commonly used name: the geometric mean. It appears in a more algebraic setting as the mean proportional $p\;$ between two numbers $a\;$ and $b\;$:
$a : p = p : b.$
Euclid VI.13 gives a geometric construction of the mean proportional:

Draw a semicircle on a diameter of length $a + b\;$ and a perpendicular to the diameter where the two segments join. The length of the perpendicular from the circumference to the diameter is exactly the geometric mean of $a\;$ and $b\;$.
(In passing, the are two more terms in Euclid VI that relate to the proportions like the above. The fourth proportional of the given numbers $a\;$, $b\;$, $c\;$ is number $x\;$ such that $ab = c/x.\;$ The third proportional of two numbers $a\;$ and $b\;$ is number $y\;$ such that $a/b = b/y.\;$ Also, this same construction is used by Euclid II.14 to construct a square of the same area as a given rectangle.)
The above construction of the mean proportional is based on a Corollary from Euclid VI.8: If in a right-angled triangle a perpendicular is drawn from the right angle to the base, then the straight line so drawn is a mean proportional between the segments of the base. However this is not the only appearance of the mean proportional in right triangle. For example, in a right triangle with the altitude to the hypotenuse drawn we may observe three similar triangles: the given one, and the smaller ones cut off by the altitude. The corollary to VI.8 is derived from the similarity of two small triangles. If we pair the big triangle with any of the smaller ones, we'll find that a leg of a right triangle is the mean proportional between its projection on the hypotenuse and the hypotenuse itself.

In fact the geometric mean makes quite frequent appearances in a variety of geometric situations. I'll mention a few.
The length of the common tangent of two circles of diameters $a\;$ and $b\;$ that are tangent externally is the geometric mean of the diameters:

The geometric mean appeared as a tangent to a circle in John Wallis' very first geometric interpretation of complex numbers:

In the framework of the See-Saw Lemma, if a semicircle is inscribed between two perpendiculars to its diameter and a transversal tangent to the semicircle cut segments of lengths $a\;$ and $b\;$ from the two lines, then the radius of the semicircle is the geometric mean of $a\;$ and $b\;$.

In one of the simplest sangaku a square is inscribed into a right triangle. The process of inscribing a square continues for two more steps with the cut off triangles. Inscribe the incircles into three similar and similarly obtained triangles. Let their radii be $a\;$, $p,\;$ $b\;$ in the decreasing order, then $p\;$ is the mean proportional of $a\;$ and $b\;$.
Let $AB\;$ be a chord in a circle and $P\;$ a point on the circle. Draw perpendiculars $PQ,\;$ $PR,\;$ and $PS\;$ from $P\;$ to $AB\;$ and the tangents to the circle at $A\;$ and $B.\;$ Then $PQ^{2} = PR\cdot PS.$
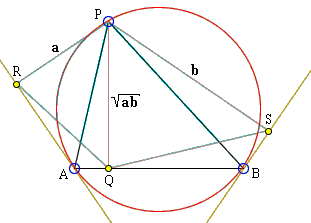
Let points $C\;$ and $D\;$ lie on a semicircle with diameter $AB.\;$ Let $E\;$ be the intersection of $AC\;$ and $BD\;$ and $F\;$ the intersection of $AD$ and $BC.\;$ Let $EF\;$ meet the semicircle in $G\;$ and $AB\;$ in $H.\;$ Then $GH^{2} = EH\cdot FH$.

[W. H. Besant, Conic Sections Treated Geometrically, George Bell & Sons, London, 1895, p. 28]. If from a point $Q\;$ tangents $QP,\;$ $QP'\;$ be drawn to a parabola, the two triangles $SPQ\;$ and $SQP'\;$ $(S\;$ the focus of the parabola), are similar, and $SQ\;$ is a mean proportional between $SP\;$ and $SP'.$
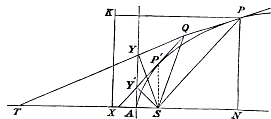
Produce $PQ\;$ to meet the axis in $T,\;$ and draw $SY,\;$ $SY'\;$ perpendicularly on the tangents. Then $Y\;$ and $Y'\;$ are points on the tangent at $A.\;$
$\begin{align} \angle SPQ &= \angle STY\\ &= \angle SYA\\ &= \angle SQP', \end{align}$
since $S, Y', Y, Q\;$ are points on a circle, and $SYA,\;$ $SQP'\;$ are in the same segment.
Also, since the tangents drawn from any point to a conic subtend equal angles at the focus, $\angle PSQ = \angle QSP';\;$ therefore the triangles $PSQ,\;$ $QSP'\;$ are similar, and
$SP:SQ = SQ:SP'.$
If two isosceles triangles $OTB\;$ and $OAT\;$ are similar, as in the diagram below, we get an easy proportion $OT/BO = AO/OT,\;$ meaning $OT\;$ is the geometric mean of $AO\;$ and $BO.\;$
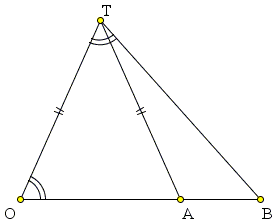
In case the common base angle equals $72^{circ}\;$ we have a dissection of the golden triangle; however, the geometric mean stays on even for pedestrian angles.
The configuration of two isosceles triangles has been used for a fast construction of the geometric mean of two line segments.
One consequence of Bui Quang Tuan's Lemma of equal areas is an assertion about the areas of triangles in this configuration:

Namely, $[BDE]^{2} = [ABD][BCE],\;$ where $[X]\;$ denotes the area of shape $X.$
- The diagonals of a trapezoid cut it into four triangles:
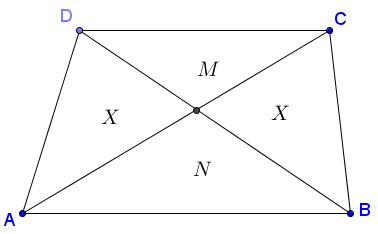
Two of them have equal areas, say $X,\;$ if the areas of the other two are $M\;$ and $N\;$ then $X=\sqrt{M\cdot N}.$
Have you seen the geometric mean elsewhere? Let me know. Thank you.
Related material
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73510195
