Pythagoras' Theorem plays an important role in geometry and in mathematics in general. On this page I'll try to collect several statements some of whose proofs depend on the Pythagorean Theorem.

The Arithmetic - Geometric Means Inequality

For a proof, assume a > b and construct a right triangle with hypotenuse (a+b)/2 and one side equal to (a-b)/2. From the Pythagorean Theorem, the remaining side will equal √ab. Since, in a right triangle, the hypotenuse is the largest side, the inequality has been proven in the case a > b. It's obviously turns into equality when a = b.

One may argue that the proof followed from an algebraic identity

In that case, the Pythagorean Theorem furnishes an intuitive geometric illustration. Just draw two touching circles with radii a/2 and b/2 as in the diagram.

(a + b)/2 is known as the arithmetic mean of the numbers a and b; √ab is their geometric mean also known as the mean proportional because if k = √ab then a/k = k/b and vice versa.

As in the case Isoperimetric Inequality this too allows for two equivalent extremal problems:

1. Among all pairs of numbers with a given product find two whose sum is minimal.
2. Among all pairs of numbers with a given sum find two whose product is maximal.

The former is often rewritten in a different form:

The Arithmetic Mean - Geometric Mean Inequality for sequences of numbers was first proven when the length of the sequence was a power of 2 and from here for an arbitrary integer. (1) also extends for an arbitrary number of positive numbers:

Actually more is true. For positive x_i's, let p be an arbitrary permutation of the set of indices {1,...,n}. Then

The Cosine Rule is an obvious generalization of the Pythagorean Theorem. However, its variant that does not use trigonometric functions is a direct consequence of the latter.

Lemma

The difference of squares of two sides of a triangle equals the difference of squares of their projections on the third side:

For a proof, use Pythagoras' Theorem twice: AB²=AH²+BH² and BC²=CH²+BH². Subtract one equation from the other.

From (2), BC² = AB² + CH² - AH². If ABC is an acute triangle then CH = AC - AH which gives

If angle A is obtuse, then CH = AC + AH and (2) yields

Stewart's Theorem

Coxeter and Greitzer remark that the theorem below was named after M.Stewart, who stated it in 1746, but was probably discovered by Archimedes about 300 B.C. However, the first known proof is by R.Simson, 1751.

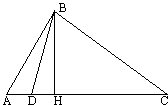
Let point D lie between the vertices A and C of ΔABC. Then

AB2·DC + BC2·AD - BD2·AC = AC·DC·AD

For the definiteness sake, let H (the foot of the altitude BH) lie between D and C, as in the diagram. Apply (3.1) to ΔBCD and (3.2) to ΔABD:

BC2 = BD2 + DC2 - 2·DC·DH AB2 = BD2 + AD2 + 2·AD·DH

Multiply the first identity by AD, the second by DC, and sum them up

BC2·AD + AB2·DC = BD2·(AD + DC) + DC2·AD + AD2·DC   = BD2·AC + AD·DC·AC

Medians

Let D be the midpoint between A and C. As usual, let a = |BC|, b = |AC|, c = |AB|, and m_b = |BD|. After division by a, Stewart's Theorem then takes the form

Which is just another way of writing Heron's formula. Thus, the two facts: Pythagoras' Theorem and Heron's formula each have an independent proof. But, in addition, each can be derived from the other.

Remark

Dr. S. Brodie has kindly prepared a demonstration of how Pythagoras' Theorem is used to construct a regular pentagon. He has also observed that the Theorem is equivalent to the famous Parallel (or Fifth) Postulate.

Finally, there is an interesting, only recently discovered, application of the theorem and an interesting puzzle the theorem helps to solve.

The area of a circle depends on a single parameter: its radius. For radius R, it equals πR². Curiously, the area of a circular ring (annulus), i.e., the shape between two concentric circles, also depends on a single parameter [Rohrer, #25].

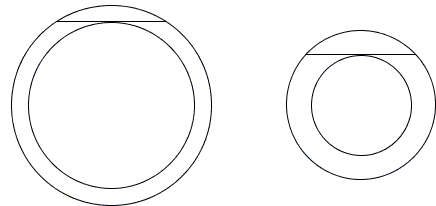
The parameter is the length (or, more conveniently, its half-length) of the chord of the outer circle tangent to the inner circle. If a denotes half the chord in question, the area of the circular ring is given by πa². To see why this is so draw the radii of the two circles to complete a right triangle. Apply the Pythagorean theorem.

It may be argued independent of the Pythagorean theorem that the area swept by a fixed length segment is the same whether it rotates around one of its points or slides as tangent to a given curve. Establishing this result then will furnish an additional proof of the Pythagorean theorem.

References

1. H. S. M. Coxeter, S. L. Greitzer, Geometry Revisited, MAA, 1967
2. R. B. Nelsen, Proofs Without Words, MAA, 1993
3. D. Rohrer, More Thought Provokers, Key Curriculum Press, 1994

|Contact| |Front page| |Contents| |Pythagorean Theorem| |Store|